Orbital

Introduction

Orbital is a Python library for constructing and visualizing curves on surfaces.

This library depends on SageMath and Povray libraries.

Installation

• Install Sage from SageMath. We assume that sage is accessible from your commandline interface.

• Install Povray. We assume that povray is accessible from your commandline interface.

• Install the orbital package:

sage -pip install orbital-surface

If you do not have root access use the following command instead:

sage -pip install --user orbital-surface

• We advice to upgrade the orbital package regularly:

sage -pip install --upgrade orbital-surface

• To execute some usecases type:

sage -python -m orbital-surface

• For showing which files were installed or for uninstalling the orbital package, use one of the following commands:

sage -pip show --files orbital-surface
sage -pip uninstall orbital-surface

Examples

For running the examples below, either copy paste the code into the Sage interface or run them as a Python module:

sage -python -m my_module_name.py

See this file for more example usecases. See the source code the io-specification of each function. The test functions might be informative for how to call each function.

Example 1: Constructing celestial surfaces

A celestial surface is a surface that contains at least two circles through almost each point. Such a surface can be embedded in the projective n-sphere S^n for some n>=2. The n-sphere S^n is a hyperquadric of signature (n+1,1). A surface in S^n of degree d that contains l circles through almost each point has celestial type: (l,d,n). We have shown that n<=7 and l is either infinity, or at most 6.

We denote the fiber product of the projective line with itself by P^1xP^1. Celestial surfaces, that contain finitely many circles through each point, are the blowup of P^1xP^1 in either 0, 2 or 4 complex conjugate points. We can parametrize such blowups by constructing a linear series of forms of bidegree (2,2) that pass through the base points.

We use get_surf() to compute from the parametrization the ideal of the surface. We look in the ideal for a quadratic form of signature (n+1,1).

# We explicitly import the required modules
#
from linear_series.class_linear_series import LinearSeries
from linear_series.class_base_points import BasePointTree
from linear_series.class_poly_ring import PolyRing
from orbital.surface_in_quadric import get_surf
from orbital.class_orb_tools import OrbTools

# We construct a parametrization of a sextic del Pezzo surface dP6
# in projective 6-space, that contains 3 conics through each point 
#
a0 = PolyRing( 'x,y,v,w', True ).ext_num_field( 't^2 + 1' ).root_gens()[0]
bp_tree = BasePointTree( ['xv', 'xw', 'yv', 'yw'] )
bp = bp_tree.add( 'xv', ( -a0, a0 ), 1 )
bp = bp_tree.add( 'xv', ( a0, -a0 ), 1 )
ls_dP6 = LinearSeries.get( [2, 2], bp_tree )
print( ls_dP6 )

# We show that dP6 can be projected into S^4
#
OrbTools.filter( None ) # enable verbose output
dct51 = get_surf( ls_dP6, ( 4+1, 1 ) )

Output:

{ 7, <<x^2*v^2 - y^2*w^2, x^2*v*w + y^2*v*w, x^2*w^2 + y^2*w^2, x*y*v^2 - y^2*v*w, x*y*v*w - y^2*w^2, y^2*v*w + x*y*w^2, y^2*v^2 + y^2*w^2>>, QQ( <a0|t^2 + 1> )[x, y, v, w] }

get_surf(316): Computing random quadrics in ideal... 
get_surf(356):           sig = (5, 1) , sig_set = set([(3, 3)]) 
get_surf(356):           sig = (5, 1) , sig_set = set([(3, 3), (2, 2)]) 
get_surf(356):           sig = (5, 1) , sig_set = set([(2, 4), (3, 3), (2, 2)]) 
get_surf(356):           sig = (5, 1) , sig_set = set([(2, 4), (3, 3), (4, 2), (2, 2)]) 
get_surf(356):           sig = (5, 1) , sig_set = set([(2, 4), (2, 3), (3, 3), (4, 2), (2, 2)]) 
get_surf(356):           sig = (5, 1) , sig_set = set([(3, 2), (3, 3), (2, 3), (2, 2), (4, 2), (2, 4)]) 
get_surf(356):           sig = (5, 1) , sig_set = set([(3, 2), (3, 3), (1, 5), (2, 3), (2, 2), (4, 2), (2, 4)]) 
get_surf(356):           sig = (5, 1) , sig_set = set([(3, 2), (3, 3), (1, 5), (2, 3), (2, 2), (5, 1), (4, 2), (2, 4)]) 
get_surf(358): Q        = [(0, 0, 1, 1, 1, 1, 1), (1, 1, 0, 1, 1, 0, 0), (0, 0, 1, 0, 1, 0, 0), (1, 0, 1, 0, 0, 0, 1), (0, 1, 0, 1, 1, 1, 1), (1, 1, 1, 1, 1, 1, 1)] 
get_surf(359): pmz_lst  = [c0^2*c1^2 - c0*s0*c1^2 + s0^2*c1^2 + c0*s0*c1*s1 + c0^2*s1^2 - c0*s0*s1^2 - c0*s0*c1 + c0*c1^2 - 2*s0*c1^2 - 2*c0^2*s1 + 2*c0*s0*s1 - c0*c1*s1 + c0*s1^2 + c0^2 - c0*s0 + c0*c1 + c1^2 - 2*c0*s1 + c0, -2*c0^2*c1^2 + c0*s0*c1*s1 - s0^2*c1*s1 - c0*s0*s1^2 + s0^2*s1^2 - c0*s0*c1 + s0^2*c1 + 2*c0*s0*s1 - 2*s0^2*s1 - c0*c1*s1 + 2*s0*c1*s1 + c0*s1^2 - 2*s0*s1^2 - c0*s0 + s0^2 + c0*c1 - 2*s0*c1 - 2*c0*s1 + 4*s0*s1 - c1*s1 + s1^2 + c0 - 2*s0 + c1 - 2*s1 + 1, s0^2*c1^2 + c0*s0*c1*s1 - c0*s0*c1 - 2*s0*c1^2 - c0*c1*s1 + c0*c1 + c1^2, c0^2*c1^2 + s0^2*c1^2 + c0^2*s1^2 + s0^2*s1^2 - 2*s0*c1^2 - 2*c0^2*s1 - 2*s0^2*s1 - 2*s0*s1^2 + c0^2 + s0^2 + c1^2 + 4*s0*s1 + s1^2 - 2*s0 - 2*s1 + 1, -c0*s0*c1^2 - c0^2*c1*s1 + c0*s0*c1*s1 - s0^2*c1*s1 + c0^2*s1^2 - c0*s0*s1^2 + c0^2*c1 - c0*s0*c1 + s0^2*c1 + c0*c1^2 - 2*c0^2*s1 + 2*c0*s0*s1 - c0*c1*s1 + 2*s0*c1*s1 + c0*s1^2 + c0^2 - c0*s0 + c0*c1 - 2*s0*c1 - 2*c0*s1 - c1*s1 + c0 + c1, -c0*s0*c1^2 + s0^2*c1^2 - c0^2*c1*s1 + c0*s0*c1*s1 - s0^2*c1*s1 + c0^2*s1^2 - c0*s0*s1^2 + s0^2*s1^2 + c0^2*c1 - c0*s0*c1 + s0^2*c1 + c0*c1^2 - 2*s0*c1^2 - 2*c0^2*s1 + 2*c0*s0*s1 - 2*s0^2*s1 - c0*c1*s1 + 2*s0*c1*s1 + c0*s1^2 - 2*s0*s1^2 + c0^2 - c0*s0 + s0^2 + c0*c1 - 2*s0*c1 + c1^2 - 2*c0*s1 + 4*s0*s1 - c1*s1 + s1^2 + c0 - 2*s0 + c1 - 2*s1 + 1] 
get_surf(360): imp_lst  = [x1^2 - 2*x0*x2 + 2*x2^2 + 3*x1*x3 + 2*x3^2 - x0*x4 + 3*x1*x4 + 2*x2*x4 + 4*x3*x4 + 3*x4^2 - 5*x1*x5 - x2*x5 - 7*x3*x5 - 7*x4*x5 + 6*x5^2, x0*x1 + 2*x0*x2 - x1*x2 - 2*x2^2 + 2*x0*x3 - x1*x3 - 2*x2*x3 - 2*x3^2 + x0*x4 - 2*x1*x4 - 2*x2*x4 - 5*x3*x4 - 3*x4^2 - 3*x0*x5 + 2*x1*x5 + 4*x2*x5 + 7*x3*x5 + 9*x4*x5 - 6*x5^2, x0^2 - 2*x0*x2 + x2^2 - 2*x0*x3 + 2*x2*x3 + x3^2 - 2*x0*x4 + 2*x2*x4 + 3*x3*x4 + 2*x4^2 + 2*x0*x5 - 2*x2*x5 - 3*x3*x5 - 4*x4*x5 + 2*x5^2, x0*x2*x4 - x1*x2*x4 - x2^2*x4 - 2*x2*x3*x4 - x0*x4^2 - x1*x4^2 - x2*x4^2 - x3*x4^2 + x0*x2*x5 + x1*x2*x5 - x2^2*x5 + x0*x4*x5 + x1*x4*x5 + x2*x4*x5 + x3*x4*x5 + 2*x4^2*x5 - 2*x4*x5^2, 2*x1*x2*x3 + 2*x2*x3^2 + 3*x1*x2*x4 + 2*x0*x3*x4 + x1*x3*x4 + 3*x2*x3*x4 + 2*x0*x4^2 + x1*x4^2 - x3*x4^2 - 2*x4^3 - 3*x1*x2*x5 - x1*x3*x5 - 5*x2*x3*x5 - 2*x3^2*x5 - 4*x0*x4*x5 - 3*x1*x4*x5 - 2*x2*x4*x5 - 4*x3*x4*x5 + 2*x1*x5^2 + 4*x2*x5^2 + 7*x3*x5^2 + 8*x4*x5^2 - 6*x5^3, 2*x0*x2*x3 - 2*x2^2*x3 - 2*x2*x3^2 + 3*x1*x2*x4 - x1*x3*x4 + x2*x3*x4 - 2*x3^2*x4 + 2*x0*x4^2 + x1*x4^2 - x3*x4^2 - 2*x4^3 - 6*x0*x2*x5 - 3*x1*x2*x5 + 6*x2^2*x5 + x1*x3*x5 + 5*x2*x3*x5 + 2*x3^2*x5 - 2*x0*x4*x5 + x1*x4*x5 + 4*x2*x4*x5 + 8*x3*x4*x5 + 4*x4^2*x5 - 2*x1*x5^2 - 4*x2*x5^2 - 7*x3*x5^2 - 8*x4*x5^2 + 6*x5^3, 4*x0*x2^2 - 4*x2^3 - x1*x2*x4 - 2*x2^2*x4 + x1*x3*x4 - x2*x3*x4 + 2*x3^2*x4 + 2*x0*x4^2 + x1*x4^2 - 4*x2*x4^2 + 3*x3*x4^2 - 2*x0*x2*x5 + x1*x2*x5 + 4*x2^2*x5 - x1*x3*x5 + 3*x2*x3*x5 - 2*x3^2*x5 - 2*x0*x4*x5 - 3*x1*x4*x5 + 8*x2*x4*x5 - 10*x3*x4*x5 - 6*x4^2*x5 + 2*x1*x5^2 - 4*x2*x5^2 + 7*x3*x5^2 + 12*x4*x5^2 - 6*x5^3, 4*x1*x2^2*x4 + 8*x2^2*x3*x4 + 7*x1*x2*x4^2 + 6*x2^2*x4^2 + x1*x3*x4^2 + 11*x2*x3*x4^2 + 2*x3^2*x4^2 + 6*x0*x4^3 + 5*x1*x4^3 + 7*x3*x4^3 - 4*x1*x2^2*x5 - 18*x1*x2*x4*x5 - 8*x2^2*x4*x5 - 22*x2*x3*x4*x5 - 14*x0*x4^2*x5 - 16*x1*x4^2*x5 - 18*x2*x4^2*x5 - 21*x3*x4^2*x5 - 14*x4^3*x5 + 8*x0*x2*x5^2 + 11*x1*x2*x5^2 - 6*x2^2*x5^2 - x1*x3*x5^2 + 3*x2*x3*x5^2 - 2*x3^2*x5^2 + 8*x0*x4*x5^2 + 9*x1*x4*x5^2 + 22*x2*x4*x5^2 + 7*x3*x4*x5^2 + 34*x4^2*x5^2 + 2*x1*x5^3 - 4*x2*x5^3 + 7*x3*x5^3 - 14*x4*x5^3 - 6*x5^4, 4*x2^2*x3^2 + 8*x2^2*x3*x4 + x1*x3^2*x4 + 2*x2*x3^2*x4 + 2*x3^3*x4 + 3*x1*x2*x4^2 + 5*x2^2*x4^2 + x0*x3*x4^2 + 2*x1*x3*x4^2 + 5*x2*x3*x4^2 + 6*x3^2*x4^2 + 4*x0*x4^3 + 3*x1*x4^3 + 7*x3*x4^3 + x4^4 - 8*x2^2*x3*x5 - x1*x3^2*x5 - 2*x2*x3^2*x5 - 2*x3^3*x5 - 8*x1*x2*x4*x5 - 10*x2^2*x4*x5 - x0*x3*x4*x5 - 6*x1*x3*x4*x5 - 17*x2*x3*x4*x5 - 17*x3^2*x4*x5 - 10*x0*x4^2*x5 - 12*x1*x4^2*x5 - 10*x2*x4^2*x5 - 34*x3*x4^2*x5 - 16*x4^3*x5 + 4*x0*x2*x5^2 + 5*x1*x2*x5^2 + x2^2*x5^2 + 4*x1*x3*x5^2 + 8*x2*x3*x5^2 + 11*x3^2*x5^2 + 6*x0*x4*x5^2 + 13*x1*x4*x5^2 + 18*x2*x4*x5^2 + 47*x3*x4*x5^2 + 45*x4^2*x5^2 - 4*x1*x5^3 - 8*x2*x5^3 - 20*x3*x5^3 - 42*x4*x5^3 + 12*x5^4] 
get_surf(361): c_lst    = [-10, 5, -5, -9, 1, -4, -4, 5, -2] 
get_surf(362): M_pol    = -5*x0^2 + 5*x0*x1 - 10*x1^2 + 40*x0*x2 - 5*x1*x2 - 35*x2^2 + 20*x0*x3 - 35*x1*x3 - 20*x2*x3 - 35*x3^2 + 25*x0*x4 - 40*x1*x4 - 40*x2*x4 - 80*x3*x4 - 55*x4^2 - 25*x0*x5 + 60*x1*x5 + 40*x2*x5 + 120*x3*x5 + 135*x4*x5 - 100*x5^2 
get_surf(375): M        = [(-5, 5/2, 20, 10, 25/2, -25/2), (5/2, -10, -5/2, -35/2, -20, 30), (20, -5/2, -35, -10, -20, 20), (10, -35/2, -10, -35, -40, 60), (25/2, -20, -20, -40, -55, 135/2), (-25/2, 30, 20, 60, 135/2, -100)] 
get_surf(376): U        = [(1.6933941857178?, -2.89541050102?, -2.653367105320?, -5.86311521468?, -7.099211920161?, 9.871055997465?), (2.498117209683007?, 0.981499026628145?, -5.36367372770992?, 0.882766141511829?, -0.376882420455794?, -1.329144377493666?), (0.2322210338038690?, -0.06231997155305?, -0.397636002501175?, -0.621489333941490?, 2.11065326066461?, 0.983821111227560?), (0.188616770955087?, 0.74593096227414?, 0.172743575353930?, -0.552555715764062?, -0.063248859624552?, -0.140814616405223?), (0.181539062149018?, -0.31031003745072?, 0.045379811107120?, -0.27834291356717?, 0.019303561944726?, -0.261410666733980?), (2.0568502102608?, 0.0577183450160?, 0.9996834066278?, 0.9614768171519?, 0.00897099245090?, 0.5103327866067?)] 
get_surf(377): J diag.  = [-1.000000000000000?, -1.000000000000000?, -1.000000000000000?, -1.000000000000000?, -1.00000000000000?, 1.000000000000000?] 

Example 2: Construct a surface by the random rotation or translation of a circle

In the previous example we constructed with get_surf() a surface X in S^n that contain two circles through each point, for given embedding dimension n and degree of X. The above method requires diagonal orthonormalization of matrices. Therefore the coefficients of polynomials that define X are large in general. In this example we use orb_product() instead, which constructs surfaces by rotating or translating a circle in S^n. The 1-parameter subgroup of automorphisms of the n-sphere are represented by a parametrized matrix. The disadvantage of this method that is gives us less control on the degree and embedding dimension. However, the advantage is that the coefficients of the defining polynomials of the constructed surfaces are small.

from orbital.prod.class_orb_input import OrbInput
from orbital.prod.orb_product import orb_product
from orbital.class_orb_tools import OrbTools 
                                          
OrbTools.filter([]) # disable verbose output 

input = OrbInput().random( 3, False )  # random input

for key in input.do.keys(): input.do[key] = False
input.do['imp'] = True # compute ideal of random surface
input.do['dde'] = True # compute degree and embedding dimension

o = orb_product( input )

print( o )

Output:

------------------------------
...............
pmat          = P0 ~~~ I ~~~ I
omat          = E[8, 2, 4, 3, 1, 6, 7, 5] ~~~ Osmpr ~~~ E[5, 2, 4, 3, 8, 6, 7, 1]
vmat          = T[0, -3, 2, -2, 0, -2, 1] ~~~ Rpapr[227, 286, 226, 309] ~~~ T[0, 3, -2, 2, 0, 2, -1]
do            = {'sng': False, 'fct': False, 'pmz': False, 'prj': False, 'imp': True, 'bpt': False, 'tst': False, 'gen': False, 'dde': True}
...............
pmz_lst       = None
prj_pmz_lst   = None
imp_lst       = [25*x4 - 11*x6 - 10*x8, x3 - x6, 50*x0 + 7*x6 - 55*x8, 75000*x1*x5 + 108459*x6^2 - 75000*x2*x7 + 69280*x6*x8 + 6900*x8^2, 2250000*x2^2 + 2250000*x5^2 - 1792921*x6^2 - 1847820*x6*x8 - 476100*x8^2, 2250000*x1^2 + 6684421*x6^2 + 2250000*x7^2 + 3332820*x6*x8 + 363600*x8^2, 3253770*x1*x6^2 - 6684421*x5*x6^2 - 2250000*x1*x2*x7 - 2250000*x5*x7^2 + 2078400*x1*x6*x8 - 3332820*x5*x6*x8 + 207000*x1*x8^2 - 363600*x5*x8^2, 16711052500*x5^2*x6^2 + 11763354681*x6^4 - 16268850000*x2*x6^2*x7 + 4482302500*x6^2*x7^2 + 8332050000*x5^2*x6*x8 + 15028079040*x6^3*x8 - 10392000000*x2*x6*x7*x8 + 4619550000*x6*x7^2*x8 + 909000000*x5^2*x8^2 + 6296452600*x6^2*x8^2 - 1035000000*x2*x7*x8^2 + 1190250000*x7^2*x8^2 + 956064000*x6*x8^3 + 47610000*x8^4]
emb           = 4
dim           = 2
deg           = 8
gen           = -1
prj_pol       = None
xyz_pol       = None
pmz_test      = None
short_str     = "['@(8,4)=(deg,emb)', {'pmat': ('P0', 'I', 'I'), 'omat': ('E[8, 2, 4, 3, 1, 6, 7, 5]', 'Osmpr', 'E[5, 2, 4, 3, 8, 6, 7, 1]'), 'vmat': ('T[0, -3, 2, -2, 0, -2, 1]', 'Rpapr[227, 286, 226, 309]', 'T[0, 3, -2, 2, 0, 2, -1]')}]"
------------------------------

From the short_str we can recover the OrbInput object, and compute more attributes as is shown in the following example.

import os
from orbital.prod.class_orb_input import OrbInput
from orbital.prod.orb_product import orb_product

os.environ['PATH'] += os.pathsep + '/home/niels/Desktop/n/app/maple/link/bin' # executable path for Maple
os.environ['PATH'] += os.pathsep + '/home/niels/Desktop/n/app/magma/link' # executable path for Magma 

s = "['@(4,3)=(deg,emb)', {'pmat': ('P0', 'I', 'I'), 'omat': ('T[1, 0, 0, 0, 0, 0, 0]', 'Orppp', 'T[-1, 0, 0, 0, 0, 0, 0]'), 'vmat': ('T[0, 1, 1, 0, 0, 0, 0]', 'Rrrrs[37, 0, 0, 0]', 'T[0, -1, -1, 0, 0, 0, 0]')}]"

input = OrbInput().set_short_str( s )
input.do['pmz'] = True
input.do['bpt'] = False
input.do['imp'] = True
input.do['dde'] = True
input.do['prj'] = True
input.do['fct'] = True  # requires access to Maple, otherwise output empty list
input.do['gen'] = True  # requires access to Maple, otherwise output value -3
input.do['sng'] = True  # requires access to Magma, otherwise output empty list
input.do['tst'] = True

o = orb_product( input )
print( o )

Output:

------------------------------
...............
pmat          = P0 ~~~ I ~~~ I
omat          = T[1, 0, 0, 0, 0, 0, 0] ~~~ Orppp ~~~ T[-1, 0, 0, 0, 0, 0, 0]
vmat          = T[0, 1, 1, 0, 0, 0, 0] ~~~ Rrrrs[37, 0, 0, 0] ~~~ T[0, -1, -1, 0, 0, 0, 0]
do            = {'sng': True, 'fct': True, 'pmz': True, 'prj': True, 'imp': True, 'bpt': False, 'tst': True, 'gen': True, 'dde': True}
...............
pmz_lst       = [4/5*c0*c1 - 3/5*s0*c1 + 7/5*c0*s1 + 6/5*s0*s1 - 12/5*c0 - 11/5*s0 - 1/5*c1 - 18/5*s1 + 28/5, 4/5*c0*c1 - 3/5*s0*c1 + 7/5*c0*s1 + 6/5*s0*s1 - 12/5*c0 - 11/5*s0 - 2*s1 + 3, 3/5*c0*c1 + 4/5*s0*c1 - 6/5*c0*s1 + 7/5*s0*s1 + 11/5*c0 - 12/5*s0, -2*s1 + 2, 0, 0, 0, 0, 4/5*c0*c1 - 3/5*s0*c1 + 7/5*c0*s1 + 6/5*s0*s1 - 12/5*c0 - 11/5*s0 - 1/5*c1 - 8/5*s1 + 13/5]
prj_pmz_lst   = [-2*s1 + 3, 4/5*c0*c1 - 3/5*s0*c1 + 7/5*c0*s1 + 6/5*s0*s1 - 12/5*c0 - 11/5*s0 - 2*s1 + 3, 3/5*c0*c1 + 4/5*s0*c1 - 6/5*c0*s1 + 7/5*s0*s1 + 11/5*c0 - 12/5*s0, -2*s1 + 2]
imp_lst       = [x7, x6, x5, x4, 100*x1^2 - 4*x0*x3 - 40*x1*x3 + 9*x3^2 - 200*x1*x8 + 44*x3*x8 + 100*x8^2, 100*x0^2 - 100*x2^2 - 4*x0*x3 - 40*x1*x3 - 91*x3^2 - 200*x1*x8 + 44*x3*x8]
emb           = 3
dim           = 2
deg           = 4
gen           = 1
prj_pol       = 25*x0^4 + 100*x0^3*x1 + 50*x0^2*x1^2 - 100*x0*x1^3 + 25*x1^4 - 50*x0^2*x2^2 - 100*x0*x1*x2^2 + 50*x1^2*x2^2 + 25*x2^4 - 24*x0^3*x3 - 40*x0^2*x1*x3 + 20*x0*x1^2*x3 + 20*x0*x2^2*x3 - 41*x0^2*x3^2 - 100*x0*x1*x3^2 + 50*x1^2*x3^2 + 50*x2^2*x3^2 + 20*x0*x3^3 + 25*x3^4
prj_pol{x0:0} = (25) * (x1^2 + x2^2 + x3^2)^2
xyz_pol       = 25*x^4 + 50*x^2*y^2 + 25*y^4 + 50*x^2*z^2 + 50*y^2*z^2 + 25*z^4 - 100*x^3 - 100*x*y^2 + 20*x^2*z + 20*y^2*z - 100*x*z^2 + 20*z^3 + 50*x^2 - 50*y^2 - 40*x*z - 41*z^2 + 100*x - 24*z + 25
pmz_test      = True
fct_lst       = 1 factors
sng_lst       = 1 components
            ~ ('[x0,x1^2 + x2^2 + x3^2]', 2*t + 1)
short_str     = "['@(4,3)=(deg,emb)', {'pmat': ('P0', 'I', 'I'), 'omat': ('T[1, 0, 0, 0, 0, 0, 0]', 'Orppp', 'T[-1, 0, 0, 0, 0, 0, 0]'), 'vmat': ('T[0, 1, 1, 0, 0, 0, 0]', 'Rrrrs[37, 0, 0, 0]', 'T[0, -1, -1, 0, 0, 0, 0]')}]"
------------------------------

We see from the output that the computed surface X is obtained by rotating a circle in the 3-sphere S^3. The surface X has degree 4 and so has its stereographic projection Y to projective 3-space P^3. The equation of Y is given by xyz_pol and its singular locus consists of an irreducible conic at infinity, without real points. The conic is known as the Euclidean absolute. The surface X is a so called Perseus cyclide and its two isolated singularities are send to the Euclidean absolute.

Example 3: Computing product of circles

A Clifford torus is a quartic surface obtained as the point-wise Hamiltonian product of two great circles in the 3-sphere S^3, where we identify S^3 with the unit quaternions. If instead of great circles we also consider little circles, then this construction leads to surfaces of degree 4 or 8 in S^3 that contain two circles through each point.

from orbital.sphere.class_sphere_input import SphereInput
from orbital.sphere.sphere_experiment import clifford
from orbital.class_orb_tools import OrbTools
OrbTools.filter( [] ) 

# create SphereInput object
inp = '[[(0, 0, 0), (0, 0, 0), (0, 0, 0), 1], [(55, 30, 0), (0,65, 0), (3/2, 0, 0), 1]]'
sinp = SphereInput().set(inp)    
sinp.bas  = False
sinp.mrk  = False
sinp.pmz  = True
sinp.fam  = True
sinp.famt = 3
sinp.stp  = 12
sinp.opa  = 3/4
sinp.ppt  = 100

# compute product of circles
plt, out  = clifford( sinp )
show( plt, frame = False )
print( out )

Output:

--- SphereInput ---
 [(0, 0, 0), (0, 0, 0), (0, 0, 0), 1]
 [(55, 30, 0), (0, 65, 0), (3/2, 0, 0), 1]
 short_input = [[(0, 0, 0), (0, 0, 0), (0, 0, 0), 1], [(55, 30, 0), (0, 65, 0), (3/2, 0, 0), 1]]
-------------------

eqn_str = (2014026851767689) * (x1^2 + x2^2 + x3^2)^4+(-1) * x0 * (-2014026851767689*x0^7 + 3438408945839472*x0^6*x1 + 5124755703563172*x0^5*x1^2 + 3098583413356464*x0^4*x1^3 - 16760366455053366*x0^3*x1^4 - 3098583413356464*x0^2*x1^5 + 5124755703563172*x0*x1^6 - 3438408945839472*x1^7 - 3092194666059840*x0^6*x2 + 18858408601592160*x0^5*x1*x2 - 3505095937654080*x0^4*x1^2*x2 - 37716817203184320*x0^3*x1^3*x2 + 3505095937654080*x0^2*x1^4*x2 + 18858408601592160*x0*x1^5*x2 + 3092194666059840*x1^6*x2 + 8821193625627136*x0^5*x2^2 + 3098583413356464*x0^4*x1*x2^2 - 40913608754234660*x0^3*x1^2*x2^2 - 6197166826712928*x0^2*x1^3*x2^2 + 19070705032753480*x0*x1^4*x2^2 - 10315226837518416*x1^5*x2^2 - 3505095937654080*x0^4*x2^3 - 37716817203184320*x0^3*x1*x2^3 + 7010191875308160*x0^2*x1^2*x2^3 + 37716817203184320*x0*x1^3*x2^3 + 9276583998179520*x1^4*x2^3 - 24153242299181294*x0^3*x2^4 - 3098583413356464*x0^2*x1*x2^4 + 22767142954817444*x0*x1^2*x2^4 - 10315226837518416*x1^3*x2^4 + 3505095937654080*x0^2*x2^5 + 18858408601592160*x0*x1*x2^5 + 9276583998179520*x1^2*x2^5 + 8821193625627136*x0*x2^6 - 3438408945839472*x1*x2^6 + 3092194666059840*x2^7 + 6184389332119680*x0^5*x1*x3 - 37716817203184320*x0^4*x1^2*x3 + 13194581207427840*x0^3*x1^3*x3 + 37716817203184320*x0^2*x1^4*x3 + 6184389332119680*x0*x1^5*x3 + 6876817891678944*x0^5*x2*x3 - 14785751688255856*x0^4*x1*x2*x3 + 13073984718391872*x0^3*x1^2*x2*x3 + 14785751688255856*x0^2*x1^3*x2*x3 + 6876817891678944*x0*x1^4*x2*x3 + 37716817203184320*x0^4*x2^2*x3 + 13194581207427840*x0^3*x1*x2^2*x3 + 12368778664239360*x0*x1^3*x2^2*x3 + 13073984718391872*x0^3*x2^3*x3 + 14785751688255856*x0^2*x1*x2^3*x3 + 13753635783357888*x0*x1^2*x2^3*x3 - 37716817203184320*x0^2*x2^4*x3 + 6184389332119680*x0*x1*x2^4*x3 + 6876817891678944*x0*x2^5*x3 - 8056107407070756*x0^5*x3^2 + 3438408945839472*x0^4*x1*x3^2 + 16979155688311444*x0^3*x1^2*x3^2 - 6536992359195936*x0^2*x1^3*x3^2 + 2193404000055588*x0*x1^4*x3^2 - 10315226837518416*x1^5*x3^2 - 3092194666059840*x0^4*x2*x3^2 - 113150451609552960*x0^3*x1*x2*x3^2 + 6597290603713920*x0^2*x1^2*x2*x3^2 + 37716817203184320*x0*x1^3*x2*x3^2 + 9276583998179520*x1^4*x2*x3^2 - 5199471844072340*x0^3*x2^2*x3^2 - 6536992359195936*x0^2*x1*x2^2*x3^2 + 11779683844239104*x0*x1^2*x2^2*x3^2 - 20630453675036832*x1^3*x2^2*x3^2 + 6597290603713920*x0^2*x2^3*x3^2 + 37716817203184320*x0*x1*x2^3*x3^2 + 18553167996359040*x1^2*x2^3*x3^2 + 9586279844183516*x0*x2^4*x3^2 - 10315226837518416*x1*x2^4*x3^2 + 9276583998179520*x2^5*x3^2 + 12368778664239360*x0^3*x1*x3^3 + 37716817203184320*x0^2*x1^2*x3^3 + 12368778664239360*x0*x1^3*x3^3 + 13753635783357888*x0^3*x2*x3^3 + 14785751688255856*x0^2*x1*x2*x3^3 + 13753635783357888*x0*x1^2*x2*x3^3 - 37716817203184320*x0^2*x2^2*x3^3 + 12368778664239360*x0*x1*x2^2*x3^3 + 13753635783357888*x0*x2^3*x3^3 - 12084161110606134*x0^3*x3^4 - 3438408945839472*x0^2*x1*x3^4 - 10987459110578340*x0*x1^2*x3^4 - 10315226837518416*x1^3*x3^4 + 3092194666059840*x0^2*x2*x3^4 + 18858408601592160*x0*x1*x2*x3^4 + 9276583998179520*x1^2*x2*x3^4 - 7291021188514376*x0*x2^2*x3^4 - 10315226837518416*x1*x2^2*x3^4 + 9276583998179520*x2^3*x3^4 + 6184389332119680*x0*x1*x3^5 + 6876817891678944*x0*x2*x3^5 - 8056107407070756*x0*x3^6 - 3438408945839472*x1*x3^6 + 3092194666059840*x2*x3^6)
Agreat  = True
Bgreat  = False
A       = [(2, 0, 0, 0, 0), (0, 2, 0, 0, 0), (0, 0, 2, 0, 0), (0, 0, 0, 2, 0), (0, 0, 0, 0, 2)]
B       = [(17/4, 3, 0, 0, -9/4), (72688803/23025140, 18544801/5756285, -16632/23885, -38400/67721, -38395467/23025140), (1126125/1151257, -139986/1151257, 2304/4777, -55440/67721, -2313773/1151257), (360/241, 240/241, 0, 418/241, -360/241), (81/85, 108/85, 154/85, 0, -9/85)]
pmzAB   = [-1/281*(44*(1685891*cos(a) + 63630*sin(a))*cos(b) - 69408*(231*cos(a) + 160*sin(a))*sin(b) + 72688803*cos(a) - 22522500*sin(a))/(12*(8676*cos(a) + 6800*sin(a) - 20485)*cos(b) + 148456*cos(a)*sin(b) + 78084*cos(a) + 122400*sin(a) - 348245), 1/281*(44*(63630*cos(a) - 1685891*sin(a))*cos(b) - 69408*(160*cos(a) - 231*sin(a))*sin(b) - 22522500*cos(a) - 72688803*sin(a))/(12*(8676*cos(a) + 6800*sin(a) - 20485)*cos(b) + 148456*cos(a)*sin(b) + 78084*cos(a) + 122400*sin(a) - 348245), -4*(12*(1700*cos(a) - 2169*sin(a))*cos(b) - 37114*sin(a)*sin(b) + 30600*cos(a) - 19521*sin(a))/(12*(8676*cos(a) + 6800*sin(a) - 20485)*cos(b) + 148456*cos(a)*sin(b) + 78084*cos(a) + 122400*sin(a) - 348245)]

To experiment copy-paste the code at the start of this file to a Sage notebook().

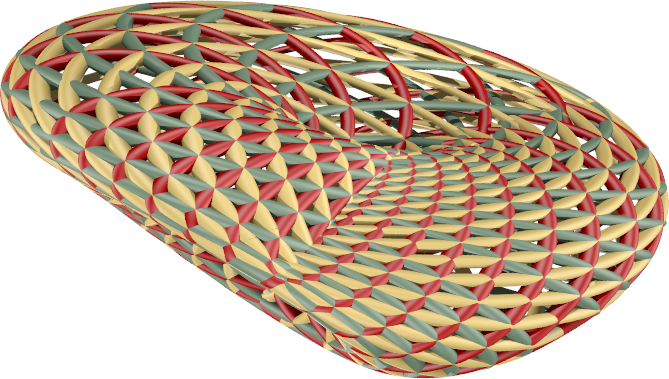
Example 4: Computing and rendering a hexagonal web of conics on a surface.

In example 1 we constructed a celestial surface in the S^4. In this example we create an image of a linear projection to 3-space of such constructed surfaces. In this example we consider a smooth del Pezzo surface in S^5 that contains 3 families of conics. The conics form a hexagonal web. We render the families of conics by using Povray.

# We explicitly import the required libraries.
#
from linear_series.class_linear_series import LinearSeries
from linear_series.class_base_points import BasePointTree
from linear_series.class_poly_ring import PolyRing

from orbital.surface_in_quadric import get_surf
from orbital.surface_in_quadric import approx_QQ
from orbital.surface_in_quadric import get_prj_mat
from orbital.surface_in_quadric import get_proj

from orbital.povray.class_pov_input import PovInput
from orbital.povray.povray import create_pov
from orbital.povray.povray_aux import get_time_str

from orbital.sage_interface import sage_QQ
from orbital.sage_interface import sage_var
from orbital.sage_interface import sage_vector
from orbital.sage_interface import sage_pi
from orbital.sage_interface import sage_set_verbose

from orbital.class_orb_tools import OrbTools

# Disable verbose output
#
sage_set_verbose( -1 )
OrbTools.filter( [] )

# Compute linear series on P^1xP^1 of bi-degree (2,2) and (1,1)
# passing through two complex conjugate base points. 
# The linear series ls_AB of bi-degree (2,2) defines a map 
# that parametrizes a surface isomorphic to the blow up of P^1xP^1 
# in two points. This surface is a del Pezzo surface of degree 6. 
# Its ideal is generated by quadratic forms.
#
a0 = PolyRing( 'x,y,v,w', True ).ext_num_field( 't^2 + 1' ).root_gens()[0]
bp_tree = BasePointTree( ['xv', 'xw', 'yv', 'yw'] )
bp = bp_tree.add( 'xv', ( -a0, a0 ), 1 )
bp = bp_tree.add( 'xv', ( a0, -a0 ), 1 )
ls_AB = LinearSeries.get( [2, 2], bp_tree )
ls_CB = LinearSeries.get( [1, 1], bp_tree )

# We compute a surface that is contained in a hyperquadric of 
# signature (6,1) and that is the projection of the surface
# parametrized by ls_AB. The quadratic form of signature (6,1)
# has associated matrix M with orthogonal diagonalization
# M=U.T*J*U, where J is a diagonal matrix. We modify J so that
# J has (-1,1,1,1,1,1,1) on its diagonal and not (1,1,1,1,1,1,-1).
#
c_lst = [-1, -1, 0, 0, 0, -1, 1, 0, -1, -1, -1] # precomputed; set to None for computing new example
dct = get_surf( ls_AB, ( 6, 1 ), c_lst )
U, J = dct['UJ']
U.swap_rows( 0, 6 );J.swap_columns( 0, 6 );J.swap_rows( 0, 6 ) 
assert dct['M'] == approx_QQ( U.T * J * U )

# In order to visualize the surface we project it to 3-space
# with a linear map defined by the matrix P. The list 
# pmz_AB_lst defines a map that parametrizes the projected surface.
# If we fix the 1st and 2nd parameter we obtain a family of conics    
# called A and B respectively.
#
approxU = approx_QQ( U )
P = get_prj_mat( 4, 7, 0 )
P[0, 6] = -1;P[3, 3] = 0;P[3, 4] = 1
P = P * approxU
f_xyz, pmz_AB_lst = get_proj( dct['imp_lst'], dct['pmz_lst'], P )

# We compute a reparametrization pmz_CB_lst of the projected surface.
# If we fix the 1st and 2nd parameter we obtain a family of conics    
# called C and B respectively. 
# See also orbital.surface_in_quadric.get_S1xS1_pmz().
#
ring = PolyRing( 'x,y,v,w,c0,s0,c1,s1' )  # construct polynomial ring with new generators
x, y, v, w, c0, s0, c1, s1 = ring.gens()
X = 1 - s0; Y = c0; V = 1 - s1; W = c1;
CB_dct = { x:X, y:Y, v:X * W + Y * V, w: X * V - Y * W }
pmz_CB_lst = [ p.subs( CB_dct ) for p in ring.coerce( ls_AB.pol_lst )]
pmz_CB_lst = list( P * dct['Q'] * sage_vector( pmz_CB_lst ) )

# In order to render the projected surface we create a PovInput object.
#
pin = PovInput()
pin.path = '/home/niels/Desktop/' + get_time_str() + '_dp6_smooth/'
pin.fname = 'orb'
pin.scale = 1
pin.cam_dct['location'] = ( 0, 0, sage_QQ( -21 ) / 10 )
pin.cam_dct['lookat'] = ( 0, 0, 0 )
pin.cam_dct['rotate'] = ( 310, 0, 0 )
pin.shadow = True
pin.light_lst = [( 0, 0, -5 ), ( 0, -5, 0 ), ( -5, 0, 0 ), ( 0, 0, 5 ), ( 0, 5, 0 ), ( 5, 0, 0 ) ]
pin.axes_dct['show'] = False
pin.axes_dct['len'] = 1.2
pin.height = 400
pin.width = 800
pin.quality = 11
pin.ani_delay = 1
pin.impl = None
pin.pmz_dct['A'] = ( pmz_AB_lst, 0 )
pin.pmz_dct['B'] = ( pmz_AB_lst, 1 )
pin.pmz_dct['C'] = ( pmz_CB_lst, 0 )
v0_lst = [ ( sage_QQ( i ) / 180 ) * sage_pi for i in range( 0, 360, 10 )]
v1_lst = [ ( sage_QQ( i ) / 180 ) * sage_pi for i in range( 0, 360, 15 )]
pin.curve_dct['A'] = {'step0':v0_lst, 'step1':v1_lst, 'prec':10, 'width':0.02}
pin.curve_dct['B'] = {'step0':v0_lst, 'step1':v1_lst, 'prec':10, 'width':0.02}
pin.curve_dct['C'] = {'step0':v0_lst, 'step1':v1_lst, 'prec':10, 'width':0.02}
col_A = ( 0.4, 0.0, 0.0, 0.0 )
col_B = ( 0.2, 0.3, 0.2, 0.0 )
col_C = ( 0.8, 0.6, 0.2, 0.0 )
pin.text_dct['A'] = [True, col_A, 'phong 0.2 phong_size 5' ]
pin.text_dct['B'] = [True, col_B, 'phong 0.2 phong_size 5' ]
pin.text_dct['C'] = [True, col_C, 'phong 0.2 phong_size 5' ]
print('pin.path =', pin.path)

# raytrace all families of conics on the projected surface using Povray.
# This takes a long time.
#
lst = create_pov( pin, ['A', 'B', 'C'] )

Output:

pin.path = /home/niels/Desktop/2018-04-04__12-42-31_dp6_smooth/