TddPy
A decision diagram based backend for tensor calculation, which is especially suitable for quantum circuit simulation.
An introduction to TDD (Tensor Network Decision Diagram) can be found at:
Installation
pip3 install tddpy
Documentation
To be written ...
Tutorials
TDD Construction
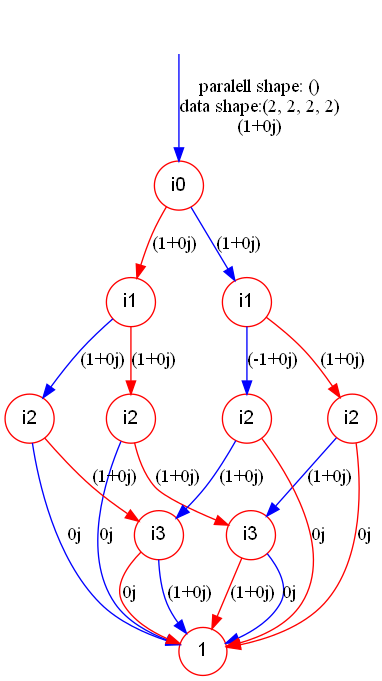
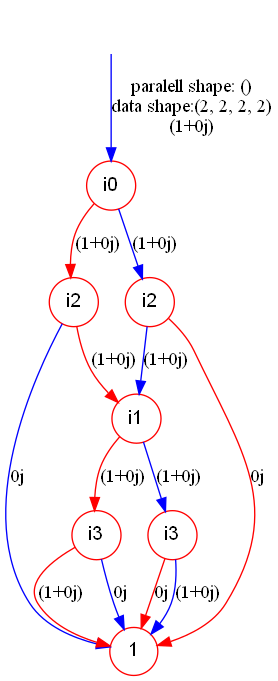
Here, we convert the CZ (controlled-Z) gate to a TDD, in the trival storage order, and output the graph picture.
import numpy as np
import tddpy
cz = np.array([[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., -1.]]).reshape((2,2,2,2))
cz_tdd = tddpy.TDD.as_tensor(cz)
print(cz_tdd.numpy())
cz_tdd.show("cz_tdd")Specifying Storage Order
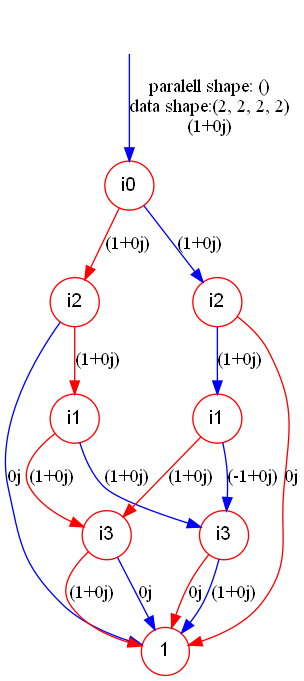
We then try to store the CZ gate in the paired storage order to get a more compact TDD. Note that a tuple of (tensor, parallel index number, storage order) is passed in as the parameter. The storage order will only influence the inner storage in TDD, not the tensor represented.
import numpy as np
import tddpy
cz = np.array([[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., -1.]]).reshape((2,2,2,2))
cz_tdd = tddpy.TDD.as_tensor((cz, 0, [0,2,1,3]))
print(cz_tdd.numpy())
cz_tdd.show("cz_tdd_compact")And the result TDD is:
Tracing
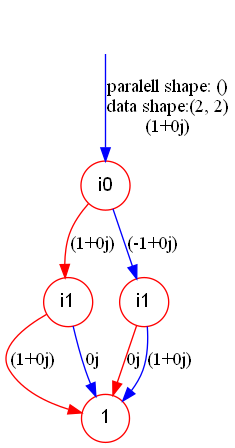
The interface for tracing and contraction (tensordot) is almost the same with that of Numpy or PyTorch. For example, we trace the second and third index of CZ:
import numpy as np
import tddpy
cz = np.array([[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., -1.]]).reshape((2,2,2,2))
cz_tdd = tddpy.TDD.as_tensor((cz, 0, [0,2,1,3]))
res_trace = cz_tdd.trace([[1],[2]])
print(res_trace.numpy())
res_trace.show("cz_tdd_traced")Contraction
The successive application of two CZ gates results in the identity gate. This can be observed by contraction of CZ tensors in the TDD form:
import numpy as np
import tddpy
cz = np.array([[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., -1.]]).reshape((2,2,2,2))
cz_tdd = tddpy.TDD.as_tensor((cz, 0, [0,2,1,3]))
res_cont = tddpy.TDD.tensordot(cz_tdd, cz_tdd, [[2,3],[0,1]])
print(res_cont.numpy())
res_cont.show("cz_tdd_cont")And the reuslt TDD is:
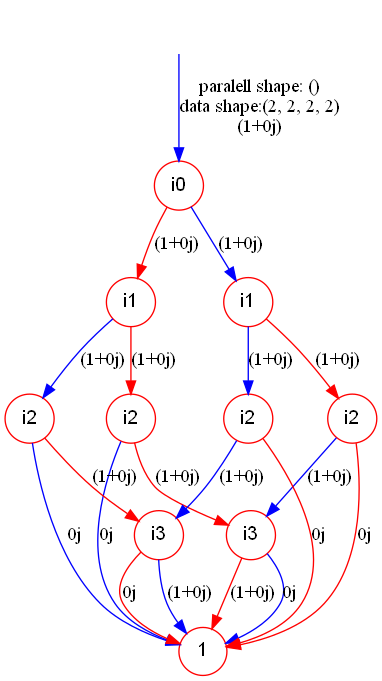
Rearrangement of Contraction
A rearrangement of remained indics from TDD A and B, after their contraction, can be specified to get the better inner storage. In the last example, we can specify the rearrangment to get the paired storage order:
import numpy as np
import tddpy
cz = np.array([[1., 0., 0., 0.],
[0., 1., 0., 0.],
[0., 0., 1., 0.],
[0., 0., 0., -1.]]).reshape((2,2,2,2))
cz_tdd = tddpy.TDD.as_tensor((cz, 0, [0,2,1,3]))
rearrangement = [True, False, True, False]
res_cont = tddpy.TDD.tensordot(cz_tdd, cz_tdd, [[2,3],[0,1]], rearrangement)
print(res_cont.numpy())
res_cont.show("cz_tdd_cont_rearranged")And the result will become much more compact:
Tensor Weight TDD
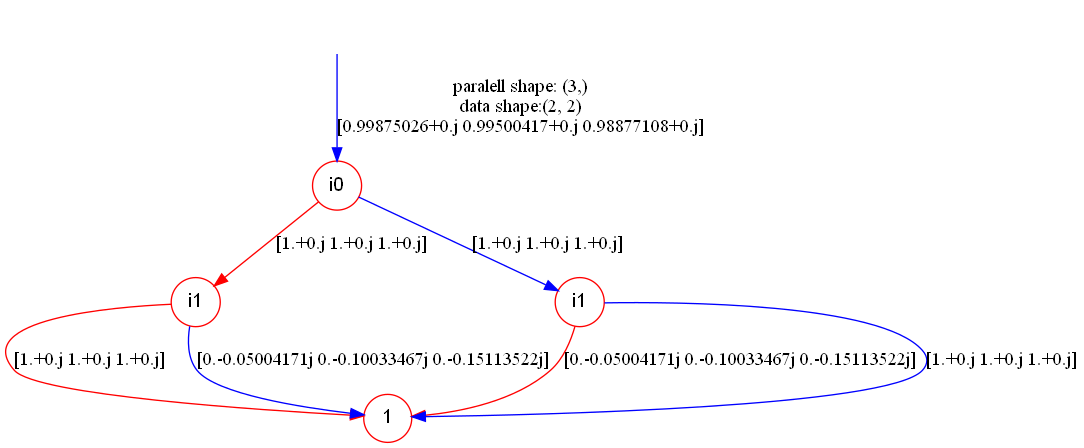
For TDDs of the same graph structure, we can "stack" them together to get the tensor weight TDD. For example, the TDD in next example represents the tensor $$ [R_x(\theta_1)\ R_x(\theta_2)\ R_x(\theta_3)]. $$
import torch
import tddpy
from tddpy.CUDAcpl import quantum_circ
theta = torch.rand((3,), dtype = torch.double)
layer1 = quantum_circ.Rx(theta)
layer1_tdd = tddpy.TDD.as_tensor((layer1, 1, []))
print(layer1_tdd.numpy())
layer1_tdd.show("tensor_weight")And the tensor weight TDD looks like
Hybrid Contraction
Contraction can be conducted among scalar weight or tensor weight TDDs. For example, we can apply the Hadamard gate (scalar weight TDD) after multiple $R_x(\theta_i)$ gates (tensor weight TDD).
import torch
import tddpy
from tddpy.CUDAcpl import quantum_circ
h_tdd = tddpy.TDD.as_tensor(quantum_circ.hadamard())
theta = torch.tensor([0.1, 0.2, 0.3], dtype = torch.double)
layer1 = quantum_circ.Rx(theta)
layer1_tdd = tddpy.TDD.as_tensor((layer1, 1, []))
res_cont = tddpy.TDD.tensordot(h_tdd, layer1_tdd, [[1],[0]])
print(res_cont.numpy())
res_cont.show("hybrid_cont_res")And the result looks like
Order Coordinator
The Order coordinator is an extra design above TDD, which provides the interface to designate the strategy for storage order and rearrangement. It is intended for auto contraction in tensor network frameworks.
Settings
The run-time settings for tddpy package can be adjusted by the method
tddpy.setting_update(thread_num, device_cuda, dtype_double, eps, gc_check_period, vmem_limit_MB)It designates the thread number in parallelism, the device for tensor weight calculation, the float number type, the float comparison EPS and garbage collection settings.
Contact
If you have any question, don't hesitate to contact lucianoxu@foxmail.com