Contents:
Introduction
A beam is a structural element that primarily resists loads applied laterally to the beam's axis (an element designed to carry primarily axial load would be a strut or column). Its mode of deflection is primarily by bending. The loads applied to the beam result in reaction forces at the beam's support points. The total effect of all the forces acting on the beam is to produce shear forces and bending moments within the beams, that in turn induce internal stresses, strains and deflections of the beam. Source: Wikipedia
About the module
This module is aimed to solve Statically Determinate, Geometrically Stable two dimensional Beam just by using 3 equations of static equilibrium.
This module supports:
- determinate 2D beam with Point Loads, Uniformly Distributed Loads, Uniformly Varying Loads, Point Moments
- Fixed or Hinged or Roller types of support conditions
- A Beam with Internal Hinge
- Bending Moment Diagram and Shear Force Diagram
Program Motivation
I studied about Beams first time in my second semester which had an included course of Applied Mechanics - I (Statics). About 10-15 marks question were sure from beams and frames in board examination. But, while practicing beam analysis questions, from past question collection, one thing that collection was lacking was solution to those questions. Not even reaction values were given. So, it would cost us 15 minutes for even simple reaction calculation error. So, I thought of making this library from that period. And, I turned this thought into action in my 3rd semester's vacation.
Installation and usage
pip install beamframe
Requirements
"numpy>=1.19",
"sympy>=1",
"matplotlib>=3"
Note All requirements will be installed automatically while installing this module.
Importing the module
Any one way of importing can be adopted
from beamframe import beam
#or
from beamframe.beam import *
Documentation
Units and Conventions
One can use and follow thier own sign conventions in this module. But, default values will have following units and sign conventions.
Sign Conventions:
- Positive x-axis for beam: increases in right hand side.
- Positive y-axis for beam: increases upward direction.
- Positive angle direction: Counter clockwise with respect to positive x-axis of beam.
- Positive moment: Counter clockwise
Standard Units:
- Length: meter
- Angle: degrees
- Load: kN
- Moment: kNm
- Load per meter: kN/m
List of all classes and arguments
| class | required arguments | optional arguments |
|---|---|---|
Beam |
length: float |
E: float, I:float |
Load |
pos: float, load: float |
inverted:bool=False |
PointLoad |
pos: float, load: float |
inverted:bool = False, inclination:float=90 |
UDL |
start: float, loadpm: float, span: float |
inverted:bool = True |
UVL |
start: float, startload: float, span: float, endload: float |
inverted: bool = True |
Reaction |
pos: float, type: str, pos_sym: str |
none |
PointMoment |
pos: float, mom: float |
ccw: bool = True |
Hinge |
pos: float |
side: str = 'l' |
Beam:
Beam is the main class to represent a beam object and perform various calculations.
Arguments
-
length(float): length of a beam -
ndivs(int): number of divisions of beam. This specifies number of points along beam in which shear force and bending moment values will be calculated.
Here are few optional keyword arguments
-
E(float)= Modulus of Elasticity of beam material -
I(float)= 2nd moment of area of the cross section of beam
Methods
| S.N | Method | Arguments | Description |
|---|---|---|---|
| 1. | fast_solve |
loads_list |
Pass list (or tuple) of all load, moment, reaction and hinge elements present in beam. This method will: 1. Calculate Reactions 2. Generate Shear and Bending Moment Equation |
| 2. | generate_graph |
which:str = 'both' , save_fig:bool = False , show_graph:bool = True, res:str = 'low' |
By default this generate will both Bending Moment Diagram(BMD) and Shear Force Diagram (SFD) stacked vertically. To obtain seperate graphs change default value which = 'both' to 'sfd' or 'bmd' To change resolution use res and accepted values are ('low', 'medium', 'high') or ('l', 'm', 'h')Note: Don't use res(values other than 'low') and show_graph=True together. It will create render error.
|
| 3. | add_loads |
load_list |
Pass list of force generating objects. This will add the net loads in x and y direction. Possible loads are (PointLoad, Reaction, UDL, UVL)
|
| 4. | add_moments |
momgen_list optional: about=0
|
Pass in list of moment generating objects like (PointLoad,Reaction, UDL, UVL, PointMoment) By default this function takes moment about origin. If you want to take moment about any other point, use Optional argument about and pass any x-coordinate value. |
| 5. | add_hinge |
hinge, mom_gens |
This method must be used iff there is hinge object in beam. A hinge object and list(or tuple) of moment generating objects are expected arguments |
| 6. | calculate_reactions |
reaction_list |
Pass in list(or tuple) of unknown reactions object to solve and assign reaction values |
| 7. | generate_shear_equation |
loads |
Pass in list(or tuple) of load generators to generate shear equation |
| 8. | generate_moment_equation |
loads |
Pass in list(or tuple) of load generators to generate moment equation |
| 9. | generate_shear_values |
loads |
Pass in list(or tuple) of load generators to generate shear force values along various points in beam specified by ndivs argument while creating beam object |
| 10. | generate_moment_values |
loads |
Pass in list(or tuple) of load generators to generate bending moment values along various points in beam specified by ndivs argument while creating beam object |
| 11. | save_data |
fname:str, fformat:str='txt' |
Saves numerical values of Shear Forces and Moment Values in text file for predefined number of points |
| 12. | generate_significant_values |
- | Generates salient values like maximum and minimum bending moment and shear force, contraflexures and other |
Note
Just first and second methods are sufficient to solve beam and generate graph. But, to keep track of ongoing process use other methods. Remember not to use
fast_solveand other methods(excluding method no. 2). Doing this will re-add all those loads you've passed again.
Example
#importing the module
from beamframe.beam import *
# to create a beam of length 5m:
b = Beam(5)
Load
Arguments:
-
pos(float): position of that netload with respect to beam coordinates's origin -
load(float): net load of that load type(for point load that is point load value, but it will be different for other loads like uvl and udl) -
inverted(bool)=False: Default direction of positive net load is in positive direction of y-axes- by default:
inverted = False(Positive Load) - use
inverted=True(indicates negative Load)
- by default:
PointLoad
Description
Subclass of class Load
Arguments
-
pos, load, inverted: inherit from super classLoad -
inclination(float)=90:unit=degreerepresents angle made by direction of net load with positive direction of beam's x axis- inclination will be positive for counter clockwise direction
- put negative inclination if you want to take angle in clockwise direction
Attributes
-
load_x: component of net load value in positive direciton of beam's x-axis -
load_y: component of net load value in positive y-direciton(upward direction)
UDL
UDL(Uniformly Distributed Load) is type of load that is combinaiton of infinite points load over certain length acting transverse to beam
Arguments:
-
start(float):Start position of UDL -
loadpm(float): Load Per meter of udl -
span(float): Total length of udl -
inverted(bool) = True: UDL facing downwards on beam- use
inverted=Falsefor upside udl
- use
Attributes
-
netload(float): total effective load of udl -
pos(float): position of effective load from - beam origin
UVL
It is that load whose magnitude varies along the loading length with a constant rate. Uniformly varying load is further divided into two types:
1. Triangular Load
2. Trapezoidal Load
Arguments
-
start:float= Start position of uvl from beam's origin along x-axis of beam coordinate system -
startload:float=unit: kN/m= Starting load/m value of uvl -
span:float= Total length of uvl object -
endload:float= Ending load/m value of uvl object -
inverted:bool= True: Default=TrueInverts the uvl object
Attributes
-
end= End coordinate of uvl object -
tload= Net load value of upper triangular part of trapezoidal or triangular load -
rload= Net load value of lower rectangular part of trapezoidal load itself -
netload= Net load of whole uvl object itself.netload = tload + rload -
netpos= Net position(coordinates) where net load of uvl acts
Reaction
Reactions are given by supports. 3 types of supports are defined for now:
hinge, roller and fixed support.
Arguments
-
pos(float): position of reaction -
type(str): any one of('roller','hinge','fixed')or('r','h','f')Representing support condition at that point. -
pos_sym(str): Symbolic variable to represent support location name
Attributes
-
rx_val, ry_val, mom_val: variables to store numerical values for reaction loads and moments -
rx_var, ry_var, mom_var: symbolic variables to store symbolic values for reactions
PointMoment
Pure moment that act at point
Arguments
-
pos: location of that point moment from beam's origin -
mom: value of that point moment -
ccw(bool) = False: counterclockwise direciton is positive value of moment,- by defalut:
ccw = Falseand given moment is positive
- by defalut:
Hinge
Internal hinges are provided in a structure to reduce statical indeterminacy of the structure. Bending moment at internal hinge is always zero. Internal hinge makes structure more flexible. It allows structure to move which reduces the reactive stresses.
Arguments
-
pos:float= Position of that internal hinge from origin of beam coordinate system -
side:str = 'l': Accepted Values =('r', 'right', 'l', 'left')- Default Value =
'l' - This side specifies which side of loads to take in order to take moment of that loads about hinge.
- Default Value =
Examples
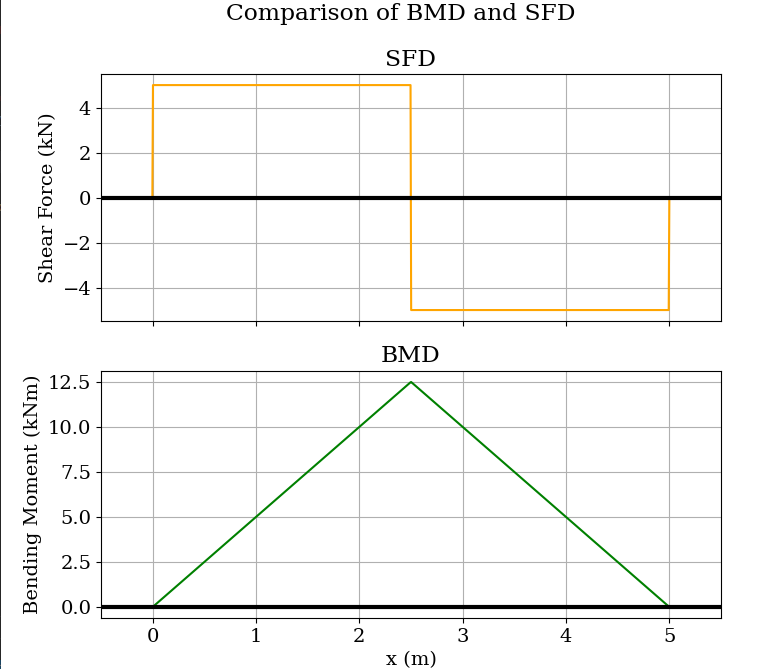
Example-1: Solving Simplest Beam
The simplest possible code to solve simply supported beam with pointload at middle of span.
#import module
from beamframe.beam import *
# create a beam of length 5m
b = Beam(5)
# create reaction and pointload objects
ra = Reaction(0, 'r', 'A')
rb = Reaction(b.length, 'h', 'B')
p = PointLoad(b.length/2, 10, inverted=True)
b.fast_solve((ra, rb, p))
b.generate_graph()
Graph:
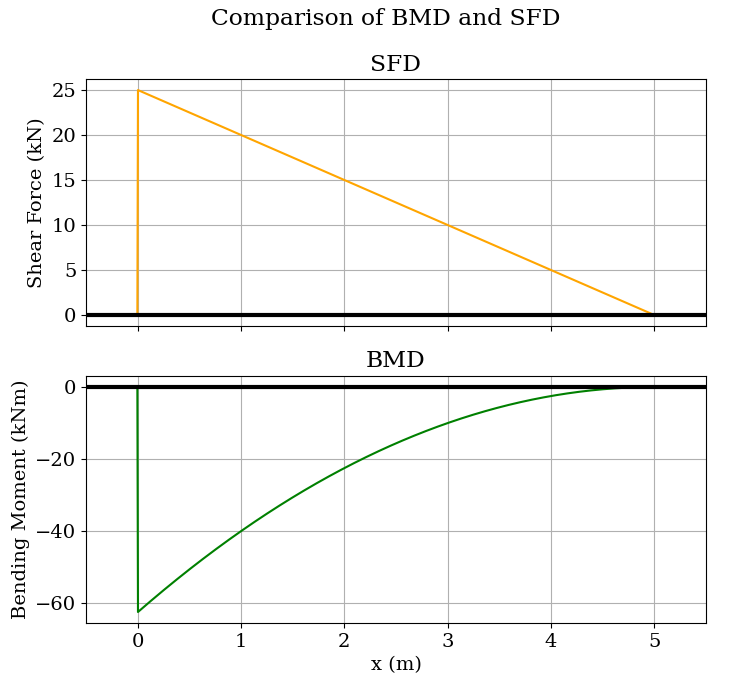
Example-2: Cantilever beam with udl
from beamframe.beam import *
# create a beam of length 5m
b = Beam(5)
# create reaction and udl object
ra = Reaction(0, 'f', 'A')
udl = UDL(0, 5, 5)
b.fast_solve((ra, udl))
b.generate_graph()
Graph:
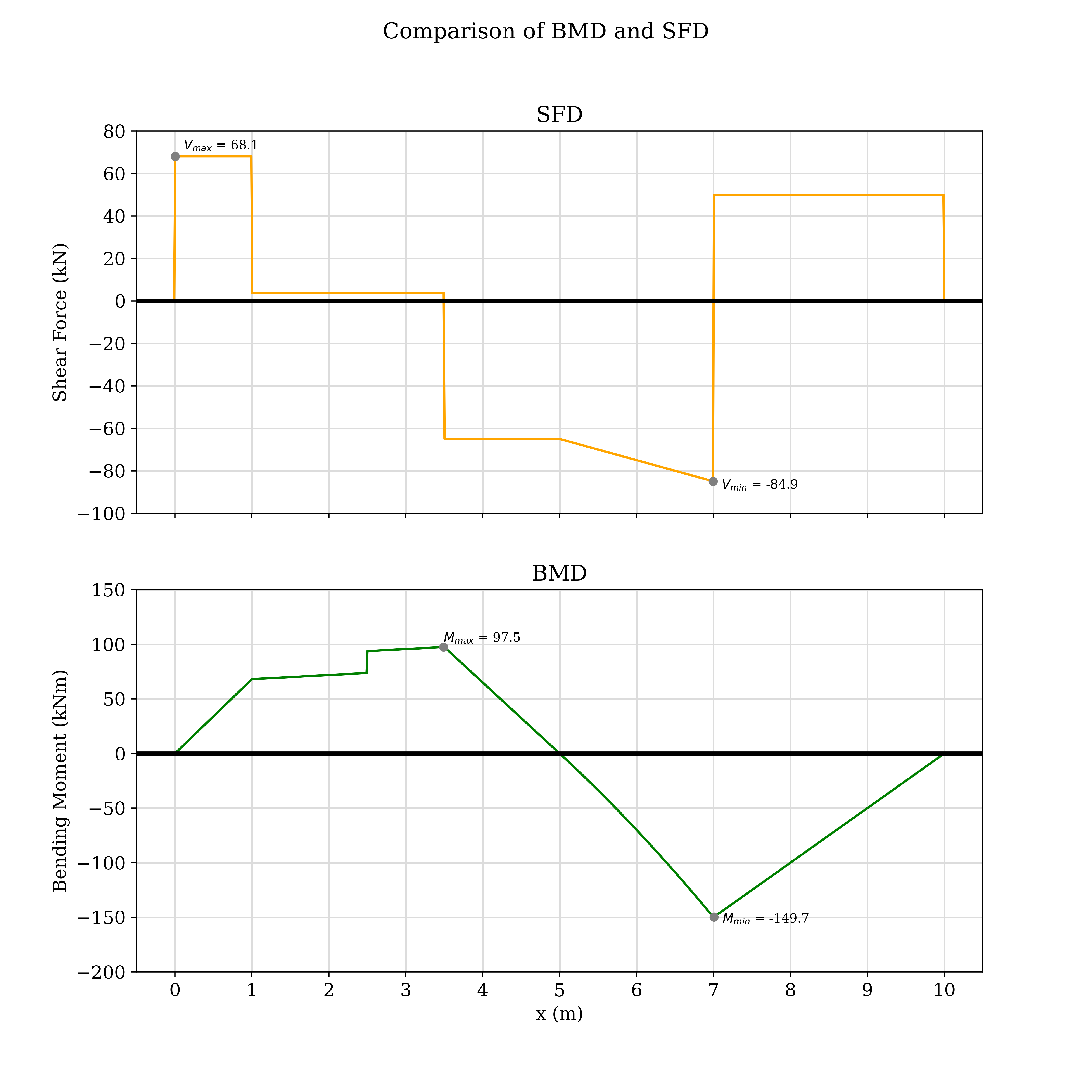
Example-3: Overhanging beam with internal hinge, and 3 supports
Note: In
b.generate_graph: usedetails=Trueto show details like max and min bending moment, max and minimum shear force.save_fig=Trueto save figure of desired quality specified by quality inres
from beamframe.beam import *
b = Beam(10)
ra = Reaction(0, 'h', 'A')
p1 = PointLoad(1,100, inverted=True, inclination=40)
m1 = PointMoment(2.5,20, ccw=False)
rd = Reaction(3.5, 'r', 'D')
h = Hinge(5, side='r')
udl = UDL(5,10,2)
rf = Reaction(7, 'r', 'F')
p2 = PointLoad(b.length, 50, inverted=True)
lds = (ra, p1, m1, rd, h, udl, rf, p2)
b.fast_solve(lds)
b.generate_graph(which='both', details=True, save_fig=True, show_graph=False, res='h')
Graph:
Any more examples required?
Contact Here