flexsolve: Flexible function solvers



What is flexsolve?
flexsolve presents a flexible set of function solvers by defining alternative tolerance conditions for accepting a solution. These solvers also implement methods like Wegstein and Aitken-Steffensen acceleration to reach solutions quicker.
Installation
Get the latest version of flexsolve from PyPI. If you have an installation of Python with pip, simple install it with:
$ pip install flexsolve
To get the git version, run:
$ git clone git://github.com/yoelcortes/flexsolve
Documentation
Flexsolve solvers can solve a variety of specifications:
- Solve x where f(x) = x (iterative):
- fixed_point: Simple fixed point iteration.
- wegstein: Wegstein's accelerated iteration method.
- aitken: Aitken-Steffensen accelerated iteration method.
- Solve x where f(x) = 0 and x0 < x < x1 (bounded):
- bisection: Simple bisection method
- false_position: Simple false position method.
- IQ_interpolation: Inverse quadratic interpolation solver (similar to scipy.optimize.brentq)
- Solve x where f(x) = 0 (open):
- secant: Simple secant method.
- aitken_secant: Secant method with Aitken acceleration.
Parameters for each solver are pretty consitent and straight forward:
- f: objective function in the form of f(x, *args).
-
x:
- Iterative solvers: Root guess. Solver begins the iteration by evaluating f(x).
-
x0, x1:
- Bounded solvers: Root bracket. Solution must lie within x0 and x1.
- Open solvers: Initial and second guess. Second guess, 'x1', is optional.
- xtol=0.: Solver stops when the root lies within xtol.
- ytol=5e-8: Solver stops when the f(x) lies within ytol of the root. Iterative solvers (which solve functions of the form f(x) = x) do not accept a ytol argument as xtol and ytol are actually mathematically equivalent.
- args=(): Arguments to pass to f.
- maxiter=50: Maximum number of iterations.
- checkiter=True: Whether to raise a Runtimer error when tolerance could not be satisfied before the maximum number of iterations.
- checkroot=False: Whether satisfying both tolerances, xtol and ytol, are required for termination.
- checkbounds=True: Whether to raise a ValueError when in a bounded solver when the root is not certain to lie within bounds (i.e. f(x0) * f(x1) > 0.).
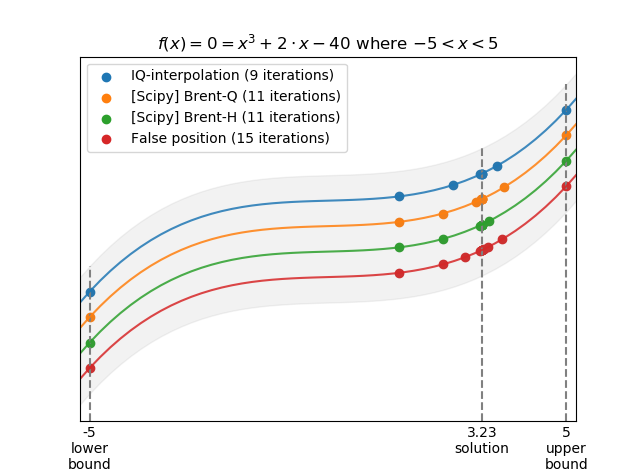
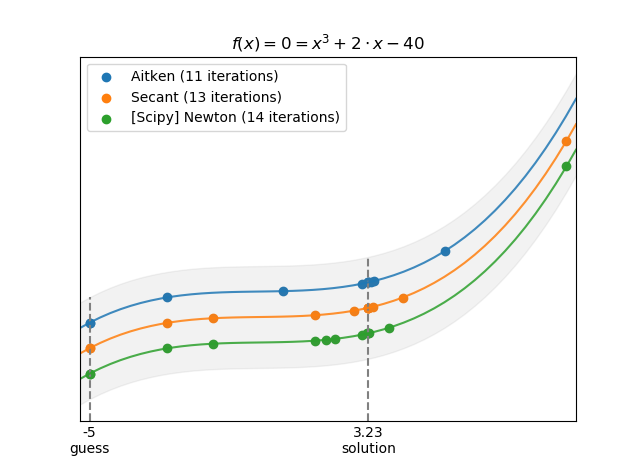
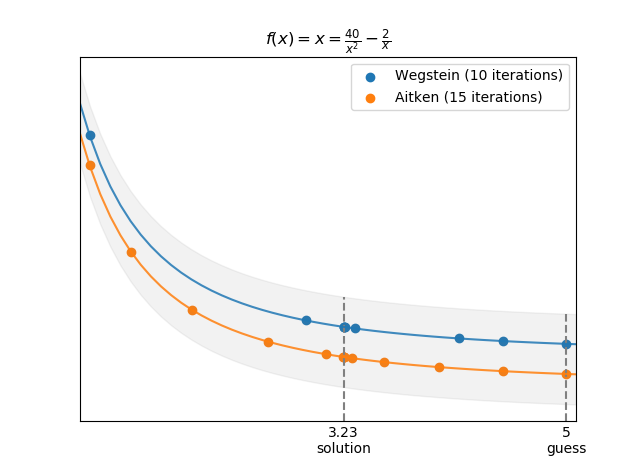
Here are some examples using flexsolve's Profiler object to test and compare different solvers. In the graphs, the points are the solver iterations and the lines represent f(x). The lines and points are offset to make them more visible (so all the points are actually on the same curve!). The shaded area is just to help us relate the points to the curve (not an actual interval):
>>> import flexsolve as flx
>>> from scipy import optimize as opt
>>> x0, x1 = [-5, 5]
>>> f = lambda x: x**3 - 40 + 2*x
>>> p = flx.Profiler(f) # When called, it returns f(x) and saves the results.
>>> opt.brentq(p, x0, x1, xtol=1e-8)
3.225240462778411
>>> p.archive('[Scipy] Brent-Q') # Save/archive results with given name
>>> opt.brenth(p, x0, x1)
3.2252404627917794
>>> p.archive('[Scipy] Brent-H')
>>> flx.IQ_interpolation(p, x0, x1)
3.225240462796626
>>> p.archive('IQ-interpolation')
>>> flx.false_position(p, x0, x1)
3.225240462687035
>>> p.archive('False position')
>>> p.plot(r'$f(x) = 0 = x^3 + 2 \cdot x - 40$ where $-5 < x < 5$')>>> p = flx.Profiler(f)
>>> x_guess = -5
>>> flx.aitken_secant(p, x_guess)
3.22524046279178
>>> p.archive('Aitken')
>>> flx.secant(p, x_guess)
3.2252404627918057
>>> p.archive('Secant')
>>> opt.newton(p, x_guess)
3.2252404627918065
>>> p.archive('[Scipy] Newton')
>>> p.plot(r'$f(x) = 0 = x^3 + 2 \cdot x - 40$')>>> # Note that x = 40/x^2 - 2/x is the same
>>> # objective function as x**3 - 40 + 2*x = 0
>>> f = lambda x: 40/x**2 - 2/x
>>> p = flx.Profiler(f)
>>> x_guess = 5.
>>> flx.wegstein(p, x_guess)
3.2252404626726996
>>> p.archive('Wegstein')
>>> flx.aitken(p, x_guess)
3.2252404627250075
>>> p.archive('Aitken')
>>> p.plot(r'$f(x) = x = \frac{40}{x^2} - \frac{2}{x}$',
... markbounds=False)
>>> # Fixed-point iteration is non-convergent for this equation,
>>> # so we do not include it hereIf you have multiple layers of functions with solvers, you can speed up calculations in flexsolve by JIT compiling them with numba. The following example benchmarks flexsolve's speed with and without compiling:
>>> import flexsolve as flx
>>> from numba import njit
>>> f = lambda x, y: x**3 - 40 + y*x
>>> g = lambda y, z: y + flx.IQ_interpolation(f, -100, 100, args=(y,))
>>> h = lambda z: z - flx.IQ_interpolation(g, -10, 10, args=(z,))
>>> # Time solver without compiling
>>> %timeit flx.IQ_interpolation(h, -5, 15)
352 µs ± 5.6 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
>>> f = njit(f)
>>> g = njit(g)
>>> h = njit(h)
>>> # First run is slower because it need to compile
>>> x = flx.IQ_interpolation(h, -5, 5)
>>> # Time solver after compiling
>>> %timeit flx.IQ_interpolation(h, -5, 5)
4.32 µs ± 79.4 ns per loop (mean ± std. dev. of 7 runs, 100000 loops each)The iterative methods for solving f(x) = x (e.g. fixed-point, Wegstain, Aitken) are capable of solving multi-dimensional problems. Simply make sure x is an array and f(x) returns an array with the same dimensions. In fact, the The Biorefinery Simulation and Techno-Economic Analysis Modules (BioSTEAM) uses flexsolve to solve many chemical engineering problems, including process recycle stream flow rates and vapor-liquid equilibrium.
Bug reports
To report bugs, please use the flexsolve's Bug Tracker at:
https://github.com/yoelcortes/flexsolve
License information
See LICENSE.txt for information on the terms & conditions for usage
of this software, and a DISCLAIMER OF ALL WARRANTIES.
Although not required by the flexsolve license, if it is convenient for you, please cite flexsolve if used in your work. Please also consider contributing any changes you make back, and benefit the community.
Citation
To cite flexsolve in publications use:
Yoel Cortes-Pena (2019). flexsolve: Flexible function solvers. https://github.com/yoelcortes/flexsolve