Description
- A collection of compact, parsimonious neuronal models, implemented in community favorite languages. Attached to a fast data driven optimization routine (numba, dask etc).
See the Documentation notebooks:
Chapter 1 / Chapter 2 / Chapter 3 / Chapter 4 / Chapter 5 / Chapter 6 / Chapter 7 / Chapter 8 / Chapter 9
| Master | Dev |
|---|---|
Optimization specific:
Assumptions, the environment for running this notebook was arrived at by building a dedicated docker file.
https://cloud.docker.com/repository/registry-1.docker.io/russelljarvis/nuo or more recently: https://cloud.docker.com/u/russelljarvis/repository/docker/russelljarvis/network_unit_opt You can run use dockerhub to get the appropriate file, and launch this notebook using Kitematic.
# Import libraries
To keep the standard running version of minimal and memory efficient, not all available packages are loaded by default. In the cell below I import a mixture common python modules, and custom developed modules associated with NeuronUnit (NU) development #!pip install dask distributed seaborn #!bash after_install.sh
goals.
given https://www.nature.com/articles/nn1352 Goal is based on this. Don't optimize to a singular point, optimize onto a cluster. Golowasch, J., Goldman, M., Abbott, L.F, and Marder, E. (2002) Failure of averaging in the construction of conductance-based neuron models. J. Neurophysiol., 87: 11291131.
Concept:
NeuronUnit uses the SciUnit-framework to test models of ion channels, neurons, and neuronal networks. https://github.com/rgerkin/papers/blob/master/neuronunit_frontiers/Paper.pdf
Documentation:
(See SciUnit documentation here first)
Presentations:
INCF Meeting (August, 2014) (Less code) https://github.com/scidash/assets/blob/master/presentations/SciUnit%20INCF%20Talk.pdf?raw=true
OpenWorm Journal Club (August, 2014) (More code) https://github.com/scidash/assets/blob/master/presentations/SciUnit%20OpenWorm%20Journal%20Club.pdf?raw=true
Examples:
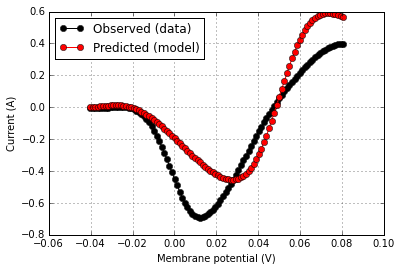
(Example 1) Validating an ion channel model's IV curve against data from a published experiment
from channelworm.ion_channel.models import GraphData
from neuronunit.tests.channel import IVCurvePeakTest
from neuronunit.models.channel import ChannelModel
# Instantiate the model
channel_model_name = 'EGL-19.channel' # Name of a NeuroML channel model
channel_id = 'ca_boyle'
channel_file_path = os.path.join('path', 'to', 'models', '%s.nml' % channel_model_name)
model = ChannelModel(channel_file_path, channel_index=0, name=channel_model_name)
# Get the experiment data from ChannelWorm and instantiate the test
doi = '10.1083/jcb.200203055'
fig = '2B'
sample_data = GraphData.objects.get(graph__experiment__reference__doi=doi,
graph__figure_ref_address=fig)
voltage, current_per_farad = sample_data.asunitedarray()
patch_capacitance = pq.Quantity(1e-13,'F') # Assume recorded patch had this capacitance;
# an arbitrary scaling factor.
current = current_per_farad * patch_capacitance
observation = {'v':voltage,
'i':current}
test = IVCurvePeakTest(observation)
# Judge the model output against the experimental data
score = test.judge(model)
rd = score.related_data
score.plot(rd['v'],rd['i_obs'],color='k',label='Observed (data)')
score.plot(rd['v'],rd['i_pred'],same_fig=True,color='r',label='Predicted (model)')score.summarize()
""" OUTPUT:
Model EGL-19.channel (ChannelModel) achieved score Fail on test 'IV Curve Test (IVCurvePeakTest)'. ===
"""
score.describe()
""" OUTPUT:
The score was computed according to 'The sum-squared difference in the observed and predicted current values over the range of the tested holding potentials.' with raw value 3.151 pA^2
"""
(Example 2) Testing the membrane potential and action potential widths of several spiking neuron models against experimental data found at http://neuroelectro.org.
import sciunit
from neuronunit import neuroelectro,tests,capabilities
import neuronunit.neuroconstruct.models as nc_models
from pythonnC.utils.putils import OSB_MODELS
# We will test cerebellar granule cell models.
brain_area = 'cerebellum'
neuron_type = 'cerebellar_granule_cell'
path = os.path.join(OSB_MODELS,brain_area,neuron_type)
neurolex_id = 'nifext_128' # Cerebellar Granule Cell
# Specify reference data for a test of resting potential for a granule cell.
reference_data = neuroelectro.NeuroElectroSummary(
neuron = {'nlex_id':neurolex_id}, # Neuron type.
ephysprop = {'name':'Resting Membrane Potential'}) # Electrophysiological property name.
# Get and verify summary data for the combination above from neuroelectro.org.
reference_data.get_values()
vm_test = tests.RestingPotentialTest(
observation = {'mean':reference_data.mean,
'sd':reference_data.std},
name = 'Resting Potential')
# Specify reference data for a test of action potential width.
reference_data = neuroelectro.NeuroElectroSummary(
neuron = {'nlex_id':neurolex_id}, # Neuron type.
ephysprop = {'name':'Spike Half-Width'}) # Electrophysiological property name.
# Get and verify summary data for the combination above from neuroelectro.org.
reference_data.get_values()
spikewidth_test = tests.InjectedCurrentAPWidthTest(
observation = {'mean':reference_data.mean,
'sd':reference_data.std},
name = 'Spike Width',
params={'injected_square_current':{'amplitude':5.3*pq.pA,
'delay':50.0*pq.ms,
'duration':500.0*pq.ms}})
# 5.3 pA of injected current in a 500 ms square pulse.
# Create a test suite from these two tests.
suite = sciunit.TestSuite('Neuron Tests',(spikewidth_test,vm_test))
models = []
for model_name in model_names # Iterate through a list of models downloaded from http://opensourcebrain.org
model_info = (brain_area,neuron_type,model_name)
model = nc_models.OSBModel(*model_info)
models.append(model) # Add to the list of models to be tested.
score_matrix = suite.judge(models,stop_on_error=True)
score_matrix.view()
Score Matrix for Test Suite 'Neuron Tests'
| Model | Spike Width | Resting Potential |
|---|---|---|
| (InjectedCurrentSpikeWidthTest) | (RestingPotentialTest) | |
| cereb_grc_mc (OSBModel) | Z = nan | Z = 4.92 |
| GranuleCell (OSBModel) | Z = -3.56 | Z = 0.88 |
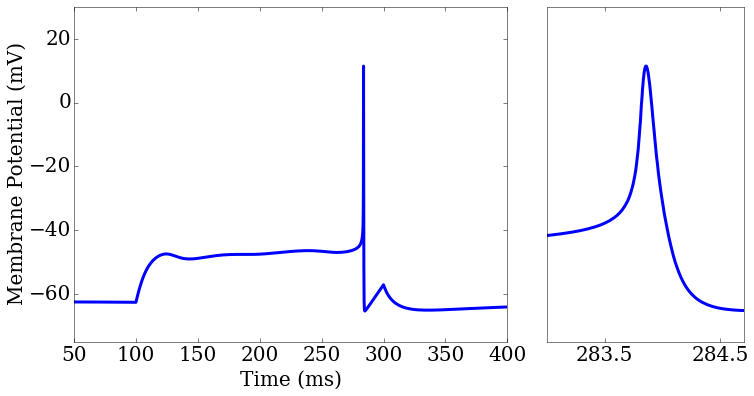
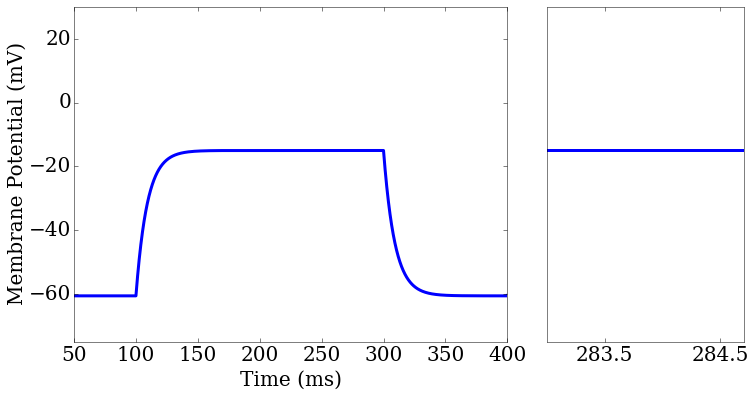
import matplotlib.pyplot as plt
ax1 = plt.subplot2grid((1,3), (0,0), colspan=2)
ax2 = plt.subplot2grid((1,3), (0,2), colspan=1)
rd = score.related_data
score_matrix[0,0].plot(rd['t'],rd['v_pred'],ax=ax1[0])
score_matrix[0,1].plot(rd['t'],rd['v_pred'],ax=ax2[0])
ax2.set_xlim(283,284.7)
Tutorial:
NeuronUnit is based on SciUnit, a discipline-agnostic framework for data-driven unit testing of scientific models. Any test script will do the following things in sequence. Most of these will be abstracted away in SciUnit or NeuronUnit modules that make things easier:
- Instantiate a model(s) from a model class, with parameters of interest to build a specific model.
- Instantiate a test(s) from a test class, with parameters of interest to build a specific test.
- Check that the model has the capabilities required to take the test.
- Make the model take the test.
- Generate a score from that test run.
- Bind the score to the specific model/test combination and any related data from test execution.
- Visualize the score (i.e. print or display the result of the test).
Here, we will break down how this is accomplished in NeuronUnit. Although NeuronUnit contains several model and test classes that make it easy to work with standards in neuron modeling and electrophysiology data reporting, here we will use toy model and test classes constructed on-the-fly so the process of model and test construction is fully transparent.
Here is a toy model class:
class ToyNeuronModel(sciunit.Model,
neuronunit.capabilities.ProducesMembranePotential):
"""A toy neuron model that is always at its resting potential"""
def __init__(self, v_rest, name=None):
self.v_rest = v_rest
sciunit.Model.__init__(self, name=name)
def get_membrane_potential(self):
array = np.ones(10000) * self.v_rest
dt = 1*ms # Time per sample in milliseconds.
vm = AnalogSignal(array,units=mV,sampling_rate=1.0/dt)
return vmThe ToyNeuronModel class inherits from sciunit.Model (as do all NeuronUnit models), and also from ProducesMembranePotential, which is a subclass of sciunit.Capability. Inheriting from a SciUnit Capability is a how a SciUnit Model lets tests know what it can and cannot do. It tells tests that the model will be implementing any method stubbed out in the definition of that Capability.
Let's see what the neuronunit.capabilities.ProducesMembranePotential capability looks like:
class ProducesMembranePotential(Capability):
"""Indicates that the model produces a somatic membrane potential."""
def get_membrane_potential(self):
"""Must return a neo.core.AnalogSignal."""
raise NotImplementedError()
def get_median_vm(self):
vm = self.get_membrane_potential()
return np.median(vm)ProducesMembranePotential has two methods. The first, get_membrane_potential is unimplemented by design. Since there is no way to know how each model will generate and return a membrane potential time series, the get_membrane_potential method in this capability is left unimplemented, while the docstring describes what the model must implement in order to satisfy that capability. In the ToyNeuronModel above, we see that the model implements it by simply creating a long array of resting potential values, and returning it as a neo.core.AnalogSignal object.
The second, get_median_vm is implemented, which means there is no need for the model to implement it again. For its implementation to work, however, the implementation of get_membrane_potential must be complete. Pre-implemented capability methods such as these allow the developer to focus on implementing only a few core interactions with the model, and then getting a lot of extra functionality for free. In the example above, once we know that the membrane potential is being returned as a neo.core.AnalogSignal, we can simply take the median using numpy. We know that the membrane potential isn't being returned as a list or a tuple or some other object on which numpy's median function won't necessarily work.
Let's construct a single instance of this model, by choosing a value for the single membrane potential argument. This toy model will now have a 60 mV membrane potential at all times:
from quantities import mV
my_neuron_model = ToyNeuronModel(-60.0*mV, name='my_neuron_model')Now we can then construct a simple test to use on this model or any other test that expresses the appropriate capabilities:
class ToyAveragePotentialTest(sciunit.Test):
"""Tests the average membrane potential of a neuron."""
def __init__(self,
observation={'mean':None,'sd':None},
name="Average potential test"):
"""Takes the mean and standard deviation of reference membrane potentials."""
sciunit.Test.__init__(self,observation,name) # Call the base constructor.
self.required_capabilities += (neuronunit.capabilities.ProducesMembranePotential,)
# This test will require a model to express the above capabilities
description = "A test of the average membrane potential of a cell."
score_type = sciunit.scores.ZScore # The test will return this kind of score.
def validate_observation(self, observation):
"""An optional method that makes sure an observation to be used as
reference data has the right form"""
try:
assert type(observation['mean']) is quantities.Quantity # From the 'quantities' package
assert type(observation['sd']) is quantities.Quantity
except Exception as e:
raise sciunit.ObservationError(("Observation must be of the form "
"{'mean':float*mV,'sd':float*mV}"))
def generate_prediction(self, model):
"""Implementation of sciunit.Test.generate_prediction."""
vm = model.get_median_vm() # If the model has the capability 'ProducesMembranePotential',
# then it implements this method
prediction = {'mean':vm}
return prediction
def compute_score(self, observation, prediction):
"""Implementation of sciunit.Test.score_prediction."""
score = sciunit.comparators.zscore(observation,prediction) # Computes a decimal Z score.
score = sciunit.scores.ZScore(score) # Wraps it in a sciunit.Score type.
score.related_data['mean_vm'] = prediction['mean'] # Binds some related data about the test run.
return scoreThe test constructor takes an observation to parameterize the test, e.g.:
from quantities import mV
my_observation = {'mean':-60.0*mV,
'sd':3.5*mV}
my_average_potential_test = ToyAveragePotentialTest(my_observation, name='my_average_potential_test')A few things happen upon test instantiation, including validation of the observation. Since the observation has the correct format (for this test class), ToyAveragePotentialTest.validate_observation will complete successfully and the test will be ready for use.
score = my_average_potential_test.judge(my_neuron_model)The sciunit.Test.judge method does several things.
-- First, it checks to makes sure that my_neuron_model expresses the capabilities required to take the test. It doesn't check to see if they are implemented correctly (how could it know?) but it does check to make sure the model at least claims (through inheritance) to express these capabilities. The required capabilities are none other than those in the test's required_capabilities attribute. Since ProducesMembranePotential is the only required capability, and the ToyNeuronModel class inherits from this capability class, that check passes.
-- Second, it calls the test's generate_prediction method, which uses the model's capabilities to make the model return some quantity of interest, in this case the median membrane potential.
-- Third, it calls the test's compute_score method, which compares the observation the test was instantiated with against the prediction returned in the previous step. This comparison of quantities is cast into a score (in this case, a Z Score), bounds to some model output of interest (in this case, the model's mean membrane potential), and that score object is returned.
-- Fourth, the score returned is checked to make sure it is of the type promised in the class definition, i.e. that a Z Score is returned if a Z Score is listed in the test's score_type attribute.
-- Fifth, the score is bound to the test that returned it, the model that took the test, and the prediction and observation that were used to compute it.
If all these checks pass (and there are no runtime errors) then we will get back a score object. Usually this will be the kind of score we can use to evaluate model/data agreement. If one of the capabilities required by the test is not expressed by the model, judge returns a special NAScore score type, which can be thought of as a blank. It's not an error -- it just means that the model, as written, is not capable of taking that test. If there are runtime errors, they will be raised during test execution; however if the optional stop_on_error keyword argument is set to False when we call judge, then it we will return a special ErrorScore score type, encoding the error that was raised. This is useful when batch testing many model and test combinations, so that the whole script doesn't get halted. One can always check the scores at the end and then fix and re-run the subset of model/test combinations that returned an ErrorScore.
For any score, we can summarize it like so:
score.summarize()
''' OUTPUT:
=== Model my_neuron_model (ToyAveragePotentialModel) achieved score 1.0 on test my_average_potential_test (ToyAveragePotentialTest)'. ===
'''and we can get more information about the score:
score.describe()
''' OUTPUT:
The score was computed according to 'the difference of the predicted and observed means divided by the observed standard deviation' with raw value 1.0
'''Reproducible Research ID
RRID:SCR_015634