skelo
An implementation of the Elo and Glicko2 rating systems with a scikit-learn-compatible interface.
The skelo package is a simple implementation suitable for small-scale rating systems that fit into memory on a single machine.
It's intended to provide a convenient API for creating Elo/Glicko ratings in a data science & analytics workflow for small games on the scale thousands of players and millions of matches, primarily as a means of feature transformation in other sklearn pipelines or benchmarking classifier accuracy.
Motivation
What problem does this package solve?
Despite there being many rating system implementations available (e.g. sublee/elo ddm7018/Elo, rshk/elo, EloPy, PythonSkills, pyglicko2, glicko2, glicko) it's hard to find one that satisfies several criteria:
- A simple and clean API that's convenient for a data-driven model development loop, for which use case the scikit-learn estimator interface is the de facto standard
- Explicit management of intervals of validity for ratings, such that as matches occur a timeseries of ratings is evolved for each player (i.e. type-2 data management as opposed to type-1 fire-and-forget ratings)
This package addresses this gap by providing rating system implementations with:
- a simple interface for in-memory data management (i.e. storing the ratings as they evolve)
- time-aware ratings retrieval (i.e. resolving a player to their respective rating at an arbitrary point in time)
- scikit-learn classifier methods to interact with the predictions in a (more) typical data science workflow
Installation
Install via the PyPI package skelo using pip:
pip3 install skeloAlternatively, a bleeding edge release is available from GitHub directly:
pip3 install git+https://github.com/mbhynes/skelo.gitFurther reference information on the API is hosted on skelo.readthedocs.io.
Quickstart
- As a quickstart, we can load and fit an
EloEstimator(classifier) on some sample tennis data:
import numpy as np
import pandas as pd
from skelo.model.elo import EloEstimator
df = pd.read_csv("https://raw.githubusercontent.com/JeffSackmann/tennis_atp/master/atp_matches_1979.csv")
labels = len(df) * [1] # the data are ordered as winner/loser
model = EloEstimator(
key1_field="winner_name",
key2_field="loser_name",
timestamp_field="tourney_date",
initial_time=19781231,
).fit(df, labels)- The ratings data are available as a
pandas DataFrameif we wish to do any further analysis on it:
>>> model.rating_model.to_frame()
key rating valid_from valid_to
0 Tim Vann 1500.000000 19781231 19790115.0
1 Tim Vann 1490.350941 19790115 NaN
2 Alejandro Gattiker 1500.000000 19781231 19790917.0
3 Alejandro Gattiker 1492.529478 19790917 19791119.0
4 Alejandro Gattiker 1485.415228 19791119 NaN
... ... ... ... ...
8462 Tom Gullikson 1483.914545 19791029 19791105.0
8463 Tom Gullikson 1478.934755 19791105 19791105.0
8464 Tom Gullikson 1489.400521 19791105 19791105.0
8465 Tom Gullikson 1498.757080 19791105 19791113.0
8466 Tom Gullikson 1490.600009 19791113 NaN- Once fit, we can transform a
DataFrameorndarrayof player/player match data into the respective ratings for each player immediately prior to the match
>>> model.transform(df, output_type='rating')
r1 r2
0 1598.787906 1530.008777
1 1548.633423 1585.653196
2 1548.633423 1598.787906
3 1445.555739 1489.089241
4 1439.595891 1502.254666
... ... ...
3954 1872.284295 1714.108269
3955 1872.284295 1698.007094
3956 1837.623245 1714.108269
3957 1837.623245 1698.007094
3958 1698.007094 1714.108269
[3959 rows x 2 columns]
- Alternatively, we could also transform a datafrom into the forecast probabilities of victory for the player
"winner_name":
>>> model.transform(df, output_type='prob')
0 0.597708
1 0.446925
2 0.428319
3 0.437676
4 0.410792
...
3954 0.713110
3955 0.731691
3956 0.670624
3957 0.690764
3958 0.476845
Length: 3959, dtype: float64
- These probabilities are also available using the
predict_probaorpredictclassifier methods, as shown below. What distinguishestransformfrompredict_probais thatpredict_probaandpredictreturn predictions that only use past data (i.e. you cannot cheat by leaking future data into the forecast), whiletransform(X, strict_past_data=False)may be used to compute ratings that "peek" into the future and could return ratings updated using match outcomes pushed (slightly) back in time to the match start timestamp. This is a specific convenience utility for non-forecasting use cases in which the match start time is a more convenient timestamp with which to index and manipulate data.
>>> model.predict_proba(df)
pr1 pr2
0 0.597708 0.402292
1 0.446925 0.553075
2 0.428319 0.571681
3 0.437676 0.562324
4 0.410792 0.589208
... ... ...
3954 0.713110 0.286890
3955 0.731691 0.268309
3956 0.670624 0.329376
3957 0.690764 0.309236
3958 0.476845 0.523155
[3959 rows x 2 columns]
>>> model.predict(df)
0 1.0
1 0.0
2 0.0
3 0.0
4 0.0
...
3954 1.0
3955 1.0
3956 1.0
3957 1.0
3958 0.0
Name: pr1, Length: 3959, dtype: float64
Available Rating System Estimators
The models in this package are the following:
-
EloEstimator- This class is a pure python implementation of a standard Elo rating system, without draws or homefield advantage
-
Glicko2Estimator
Extended Usage Examples
Synthetic Data
We can use a convenience utility for generating match data from players with normally distributed ratings. The below example shows a simple usage of this utility:
import pandas as pd
import matplotlib.pyplot as plt
import skelo.utils.elo_data as data_utils
from skelo.model.elo import EloEstimator
# Generate some sample constant ratings & match data
ratings = data_utils.generate_constant_ratings(num_players=10, sigma=500)
matches = pd.DataFrame(data_utils.generate_constant_game_outcomes(ratings, num_timesteps=100))
# Fit the model using numpy arrays
X = matches.values[:, :3] # player1, player2, match timestamp
y = matches.values[:, -1] # match outcome
model = EloEstimator().fit(X, y)
# Get a dataframe of the estimated ratings over time from the fitted model
ratings_est = model.rating_model.to_frame()
# Compare the ratings estimate over time
ts_est = ratings_est.pivot_table(index='valid_from', columns='key', values='rating')
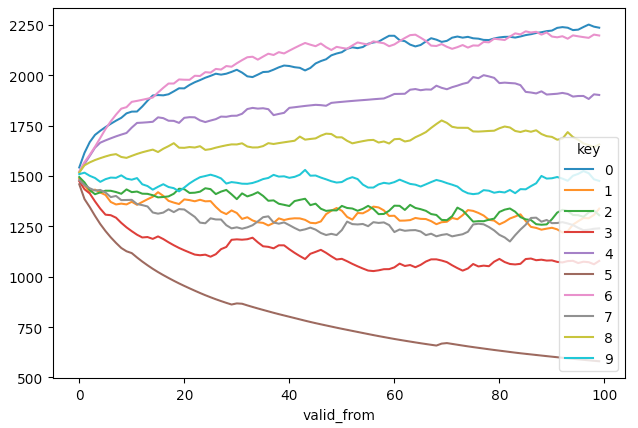
ts_est.plot()The estimated ratings will exhibit convergence profiles (players with extremal low or high ratings take longer to converge).
Please note that while the actual original ratings are unlikely to be determined by the fitting procedure, the relative difference between the ratings should be preserved, within the noise band of the chosen value of k (by default: 20)
Example Tennis Ranking
import numpy as np
import pandas as pd
from skelo.model.elo import EloEstimator
from sklearn.metrics import precision_score
# Download a dataframe of example tennis data from JeffSackmann's ATP match repository (thanks Jeff!)
def load_data():
df = pd.concat([
pd.read_csv("https://raw.githubusercontent.com/JeffSackmann/tennis_atp/master/atp_matches_1979.csv"),
pd.read_csv("https://raw.githubusercontent.com/JeffSackmann/tennis_atp/master/atp_matches_1980.csv"),
], axis=0)
# Do some simple munging to get a date and a match outcome label
df["tourney_date"] = pd.to_datetime(df['tourney_date'], format='%Y%m%d')
# For measuring classifier calibration linearity, it's better to have both true and false
# labels in the dataset, so we relabel the order of (winner, loser) to just be (player1, player2)
order_mask = (df["winner_name"] < df["loser_name"])
df["p1"] = ""
df["p2"] = ""
df["label"] = 1
df.loc[order_mask, "p1"] = df.loc[order_mask, "winner_name"]
df.loc[~order_mask, "p1"] = df.loc[~order_mask, "loser_name"]
df.loc[order_mask, "p2"] = df.loc[order_mask, "loser_name"]
df.loc[~order_mask, "p2"] = df.loc[~order_mask, "winner_name"]
df.loc[~order_mask, "label"] = 0
return df
df = load_data()
player_counts = pd.concat([df["p1"], df["p2"]], axis=0).value_counts()
players = player_counts[player_counts > 5].index
mask = (df["p1"].isin(players) & df["p2"].isin(players))
X = df.loc[mask]
# Create a model to fit on a dataframe.
# Since our match data has np.datetime64 timestamps, we specify an initial time explicitly
model = EloEstimator(
key1_field="p1",
key2_field="p2",
timestamp_field="tourney_date",
initial_time=np.datetime64('1979', 'Y'),
).fit(X, X["label"])
# Retrieve the fitted Elo ratings from the model
ratings_est = model.rating_model.to_frame()
ts_est = ratings_est.pivot_table(index='valid_from', columns='key', values='rating').ffill()
idx = ts_est.iloc[-1].sort_values().index[-5:]
ts_est.loc[:, idx].plot()This should result in a figure like the one below, showing the 5 highest ranked (within the Elo system) players based on this subset of ATP matches:
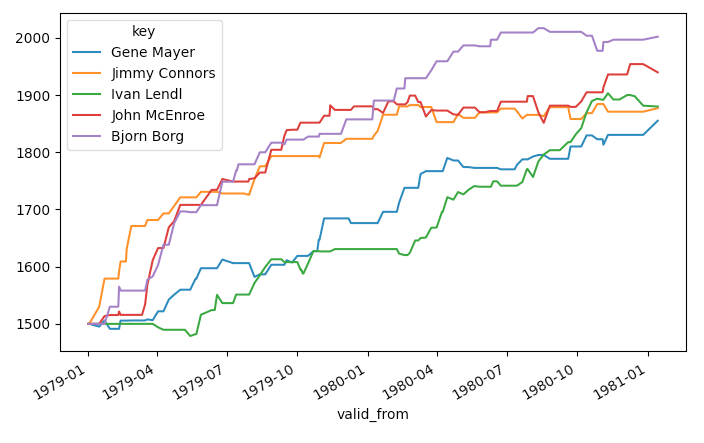
Example Tennis Ranking - Elo ratings using the sklearn API
While the ratings are interesting to visualize, the accuracy of the rating system's predictions are more important.
For determining the performance of a classifier, the sklearn API and model utilities provide simple tools for us.
Below we calculate the classification metrics of the Elo system using only the 1980 data, where each prediction for a match uses only the outcomes of previous matches:
>>> from sklearn.metrics import classification_report
>>> mask = (X["tourney_date"] > "1980-01-01")
>>> print(classification_report(X.loc[mask, "label"], model.predict(X.loc[mask])))
precision recall f1-score support
0 0.692 0.704 0.698 1782
1 0.700 0.689 0.694 1792
accuracy 0.696 3574
macro avg 0.696 0.696 0.696 3574
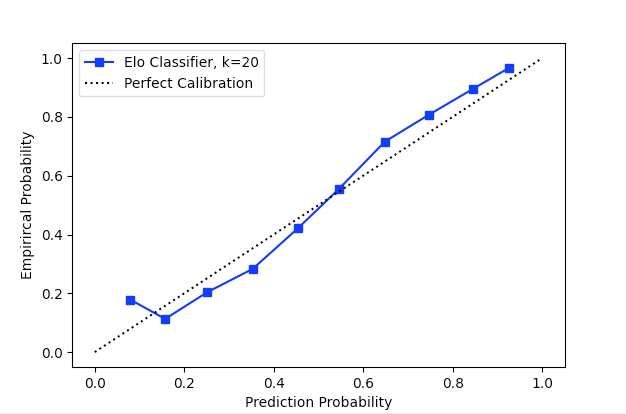
weighted avg 0.696 0.696 0.696 3574Finally, we should inspect the calibration curve of the classifier to verify its linearity (or lack thereof!):
import matplotlib.pyplot as plt
from sklearn.calibration import calibration_curve
prob_true, prob_pred = calibration_curve(
X.loc[mask, "label"],
model.predict_proba(X.loc[mask]).values[:, 0],
n_bins=10
)
plt.plot(prob_pred, prob_true, label=f"Elo Classifier, k={model.rating_model.default_k}", marker='s', color='b')
plt.plot([0, 1], [0, 1], label="Perfect Calibration", ls=":", color='k')
plt.xlabel("Predicted Probability")
plt.ylabel("Empirical Probability")
plt.legend()
It's interesting to note that the calibration curve is not strictly linear, but rather has a slight but noticeable sigmoidal shape. If you plan on doing anything with the Elo predictions in aggregate, you may want to consider calibrating the classifier output.
Example Paramter Tuning
We can now also use the sklearn utilities for parameter tuning, similar to any other forecasting model.
The below example trains several instances of the Elo ratings model with different values of k to find value that maximizes prediction accuracy during the ATP matches for 1980.
Please note that the EloModel.predict() method only uses past information available at each match, such that there is no leakage of information from the future in the model's forecasts.
from sklearn.model_selection import GridSearchCV
clf = GridSearchCV(
model,
param_grid={
'default_k': [
10, 15, 20, 25, 30, 35, 40, 45, 50,
]
},
cv=[(X.index, X.index[len(X)//2:])],
).fit(X, X['label'])
results = pd.DataFrame(clf.cv_results_)This should produce a result like the following:
>>> results.sort_values('rank_test_score').head(5).T
2 4 1 6 8
mean_fit_time 0.193156 0.172773 0.490719 0.162793 0.045234
std_fit_time 0.0 0.0 0.0 0.0 0.0
mean_score_time 0.269005 0.304881 0.336428 0.288607 0.06117
std_score_time 0.0 0.0 0.0 0.0 0.0
param_default_k 20 30 15 40 50
params {'default_k': 20} {'default_k': 30} {'default_k': 15} {'default_k': 40} {'default_k': 50}
split0_test_score 0.678779 0.677115 0.67656 0.675451 0.675451
mean_test_score 0.678779 0.677115 0.67656 0.675451 0.675451
std_test_score 0.0 0.0 0.0 0.0 0.0
rank_test_score 1 2 3 4 4
Example Tennis Ranking - Glicko2 ratings using the sklearn API
The Glicko2 implementation that we wrap has no hyperparameters to tune other than the 3-tuple to provide as the initial_value for a player; namely the initial values of the rating, the rating deviation, and the volatility.
(However the persnickety reader should note there are quite a lot of magic numbers in both the Glicko and Glicko2 papers that should probably constitute hyperparameters---these aren't available to tune simply because the available Glicko{1,2} implementations do not expose an interface that allows for tuning them. Beggars can't be choosers, as they say...)
import numpy as np
from skelo.model.glicko2 import Glicko2Estimator
from sklearn.model_selection import GridSearchCV
model = Glicko2Estimator(
key1_field="p1",
key2_field="p2",
timestamp_field="tourney_date",
initial_time=np.datetime64('1979', 'Y'),
)
clf = GridSearchCV(
model,
param_grid={
'initial_value': [
(1500., 200., 0.06),
(1500., 350., 0.06),
(1500., 500., 0.06),
(1500., 750., 0.06),
]
},
cv=[(X.index, X.index[len(X)//2:])],
).fit(X, X['label'])
results = pd.DataFrame(clf.cv_results_)We can now compare the best Glicko2 models with the Elo above and note that our test period forecasting accuracy has improved from 67.8% to 69.3%:
>>> results.sort_values('rank_test_score').head(2).T
3 2
mean_fit_time 0.212466 0.217531
std_fit_time 0.0 0.0
mean_score_time 0.068816 0.083714
std_score_time 0.0 0.0
param_initial_value (1500.0, 750.0, 0.06) (1500.0, 500.0, 0.06)
params {'initial_value': (1500.0, 750.0, 0.06)} {'initial_value': (1500.0, 500.0, 0.06)}
split0_test_score 0.693204 0.692649
mean_test_score 0.693204 0.692649
std_test_score 0.0 0.0
rank_test_score 1 2Development Setup
If you would like to contribute to this repository, please open an issue first to document the extension or modification you're interested in contributing.
dev scripts
The dev script (and other scripts in bin) contain convenience wrappers for some common development tasks:
-
Installing Dependencies. To set up a local development environment with dependencies, use:
./dev up
This will create a
.venvdirectory in the project root and install the required python packages. -
Running Tests. To run the project tests with the virtual environment's
pytest, use:./dev test
Arguments to
pytestcan be supplied to this script as well, to e.g. limit the tests to a particular subset. -
Packaging for PyPI. The package-building and upload process is wrapped with the following commands:
./dev package ./dev upload --test ./dev upload
Creating an RatingEstimator
The available models extend the skelo.model.RatingEstimator class which implements the sklearn wrapper interface around a skelo.model.RatingModel instance.
To create a new classifier, it's necessary to:
- Extend the
RatingModelto implement the rating update formulas through the methods:-
evolve_rating(r1, r2, label), which computes a new rating given the players' previous ratings,r1andr2, prior to a match with outcomelabel -
compute_prob(r1, r2), which computes the probability of victory of a player with ratingr1over a player with ratingr2
-
class EloModel(RatingModel):
def __init__(self, default_k=20, k_fn=None, initial_value=1500, initial_time=0, **kwargs):
super().__init__(initial_value=float(initial_value), initial_time=initial_time)
# Set all hyperparameters as explicit attributes, such that sklearn's CV utilities work
self.default_k = default_k
self.k = k_fn or (lambda _: default_k)
def evolve_rating(self, r1, r2, label):
exp = self.compute_prob(r1, r2)
return r1 + self.k(r1) * (label - exp)
@staticmethod
def compute_prob(r1, r2):
diff = (r2 - r1) / 400.0
prob = 1.0 / (1 + 10**diff)
return prob- Extend the
RatingEstimatorto wrap the newRatingModelsubclass and specify the list ofRatingModelattributes that should be considered hyperparamters when dynamically building aRatingsModelin the estimator'sfitmethod
class EloEstimator(RatingEstimator):
# Set this to the appropriate RatingModel:
RATING_MODEL_CLS = EloModel
# Include all tunable hyperparameter attributes of the RatingModel here:
RATING_MODEL_ATTRIBUTES = [
'default_k',
'k_fn',
'initial_value',
'initial_time',
]
def __init__(self, key1_field=None, key2_field=None, timestamp_field=None, default_k=20, k_fn=None, initial_value=1500, initial_time=0, **kwargs):
super().__init__(
key1_field=key1_field,
key2_field=key2_field,
timestamp_field=timestamp_field,
initial_value=initial_value,
initial_time=initial_time,
**kwargs
)
# These must be set as estimator attributes
self.default_k = default_k
self.k_fn = k_fnPlease note that a rating can be anything, so long as it's convenient and can support the above call signatures to create a new rating object like-for-like from existing rating objects.
For example, our EloModel implementation uses a plain float, and the Glicko2Model uses a 3-tuple for the 3 generative parameters for a player's rating.