surrkick
Black-hole kicks from numerical-relativity surrogate models
Binary black holes radiate linear momentum in gravitational waves as they merge. Recoils imparted to the black-hole remnant can reach thousands of km/s, thus ejecting black holes from their host galaxies. We exploit recent advances in gravitational waveform modeling to quickly and reliably extract recoils imparted to generic, precessing, black hole binaries.
Our procedure uses a numerical-relativity surrogate model to obtain the gravitational waveform given a set of binary parameters, then from this waveform we directly integrate the gravitational-wave linear momentum flux.
This entirely bypasses the need of fitting formulae which are typically used to model black-hole recoils in astrophysical contexts. We provide a thorough exploration of the black-hole kick phenomenology in the parameter space, summarizing and extending previous numerical results on the topic.
Our extraction procedure is made publicly available as a module for the Python programming language named surrkick. Kick evaluations take 0.1s on a standard off-the-shelf machine, thus making our code ideal to be ported to large-scale astrophysical studies.
Credits
When using surrkick in any published work, please cite the paper describing its implementation:
- Black-hole kicks from numerical-relativity surrogate models. Davide Gerosa, Francois Hebert, Leo C. Stein. arXiv:1802.04276
The code is developed and maintained by Davide Gerosa and Francois Hebert. We thank Jonathan Blackman, Chad Galley, Mark Scheel, Ulrich Sperhake, Leo Stein, Saul Teukolsky and Vijay Varma for various discussions and technical help.
Releases
Stable version released together with the first arxiv submission of arXiv:1802.04276.
Installation
surrkick is a python module, uploaded to the Python Package index. Installation is as easy as
pip install surrkick
The SXS surrogate model NRSur7dq2 and a few other dependencies will be installed together with surrkick. If you don't have it already, you might need to manually install numpy beforehand (that's pip install numpy).
You can try some functionalities with
import surrkick
surrkick.plots.minimal()
Main functions
The core of the code consists of a single class, surrkick, whose methods allow to extract radiated energy, linear momentum (kicks) and angular momentum from the underlying waveform approximant. The main methods are:
-
sur(): Instance of the surrogate class from NRSur7dq2 -
q: Binary mass ratio 0.5<=q<=1 (Default: q=1). -
chi1: Spin vector of the heavier BH at t_ref (Default chi1=[0,0,0]). -
chi2: Spin vector of the lighter BH at t_ref (Default chi2=[0,0,0]). -
t_ref: Reference time -4500<=t_ref/M<=-100 (Default t_ref/M=100). -
times: Time nodes -4500<=t_i/M<=-100 -
lmax: Largest available l-mode (lmax=4 in NRSur7dq2). -
h(l,m): Modes of the complex GW strain. -
hdot(l,m): Modes of the time derivative of the GW strain. -
dEdt: Energy flux dE/dt. -
Eoft: Radiated energy profile E(t). -
Erad: Total radiated energy. -
Moft: Mass profile M(t). -
Mfin: Mass of the remnant BH. -
dPdt: Linear momentum flux dP/dt. -
Poft: Radiated linear momentum profile P(t). -
Prad: Total radiated linear momentum. -
voft: Recoil velocity profile v(t). -
kickcomp: Kick velocity, vector. -
kick: Kick velocity, magnitude vk -
kickdir: Kick velocity, unit vector. -
dJdt: Angular momentum flux dJ/dt. -
Joft: Radiated angular momentum profile J(t). -
Jrad: Total radiated angular momentum. -
xoft: Center-of-mass trajectory x(t).
The class plots contains script to reproduce all figures and results in
arXiv:1802.04276.
You can explore its methods with, e.g. help(surrkick.plots).
Test
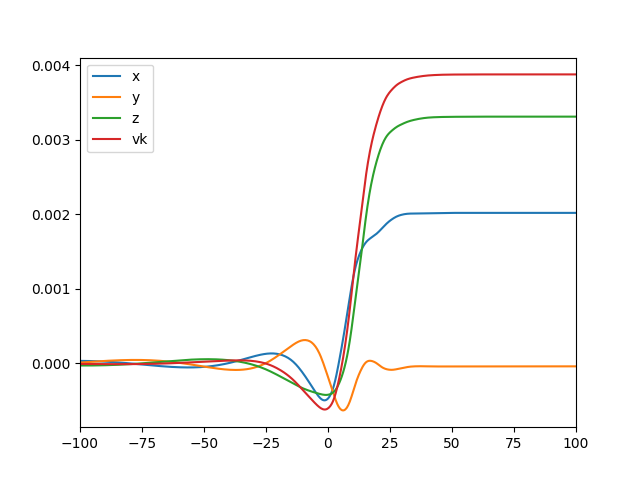
The source code for the surrkick.plots.minimal() method mentioned above is
import surrkick
import matplotlib.pyplot as plt
sk=surrkick.surrkick(q=0.5,chi1=[0.8,0,0],
chi2=[-0.8,0,0])
print "vk/c=", sk.kick
plt.plot(sk.times,sk.voft[:,0],label="x")
plt.plot(sk.times,sk.voft[:,1],label="y")
plt.plot(sk.times,sk.voft[:,2],label="z")
plt.plot(sk.times,surrkick.project(sk.voft,
sk.kickdir),label="vk")
plt.xlim(-100,100)
plt.legend()
plt.show()
If you try it, you should get a printout that reads vk/c= 0.00387... and this plot: