wendy
A one-dimensional gravitational N-body code.
Overview
wendy solves the one-dimensional gravitational N-body problem to machine precision with an efficient algorithm [O(log N) / particle-collision]. Alternatively, it can solve the problem with approximate integration, but with exact forces.
Author
Jo Bovy (University of Toronto): bovy - at - astro - dot - utoronto - dot - ca
Installation
Install the latest release using
pip install wendy
or clone/fork/download the repository and install using
sudo python setup.py install
or locally using
python setup.py install --user
The behavior of the parallel sorting algorithm used when setting sort='parallel' in the approximate version of the N-body code (approx=True) is controlled by a few compilation-time variables: PARALLEL_SERIAL_SORT_SWITCH, which sets the length of an array below which the serial sort is used, PARALLEL_SERIAL_MERGE_SWITCH, which sets the length of an array below which a serial merge is used (as part of the mergesort sorting algorithm used), and PARALLEL_SORT_NUM_THREADS, the number of threads used in the parallel sorting algorithm. By default, these are set to PARALLEL_SERIAL_MERGE_SWITCH=10000, PARALLEL_SERIAL_MERGE_SWITCH=50000, and PARALLEL_SORT_NUM_THREADS=32, which appear to work well. Significant speed-ups can be obtained by optimizing these for your system and specific problem. They can be set to different values by running, e.g.,
export CFLAGS="$CFLAGS -D PARALLEL_SERIAL_SORT_SWITCH=10 -D PARALLEL_SERIAL_MERGE_SWITCH=10 -D PARALLEL_SORT_NUM_THREADS=2"
before compiling the code (if you are trying to change them, make sure to force a re-compilation by removing the build/ directory).
Usage
Use wendy.nbody to initialize a generator object for initial (x,v) with masses m. The generator then returns the state of the system at equally-spaced time intervals:
g= wendy.nbody(x,v,m,0.05) # delta t = 0.05
next_x, next_v= next(g) # at t=0.05
next_x, next_v= next(g) # at t=0.10
...
The generator initialization with wendy.nbody has options to (a) solve the problem exactly or not using approx=, (b) include an external harmonic oscillator potential omega^2 x^2 / 2 with omega= (both for exact and approximate solutions), and (c) include an arbitrary external force F(x,t) (using ext_force=, only for the approximate solution).
Examples
You can run these without installing wendy by clicking on and navigating to the
examples/ directory. Note that some of the movies might fail to be rendered on the binder webpage, so you might want to skip those when running the notebooks (or changing the subsamp input for them).
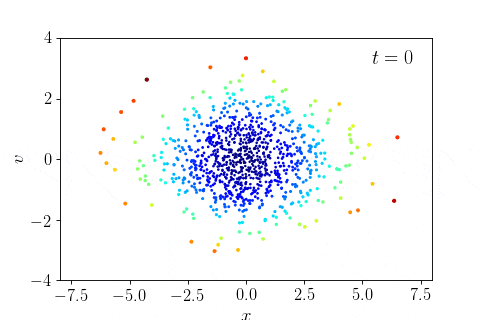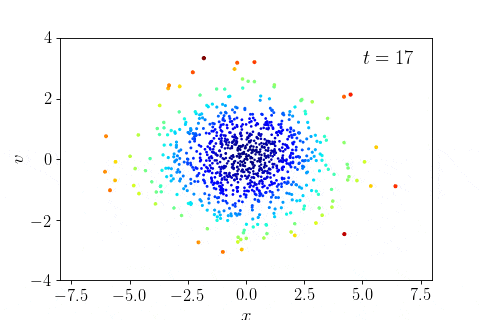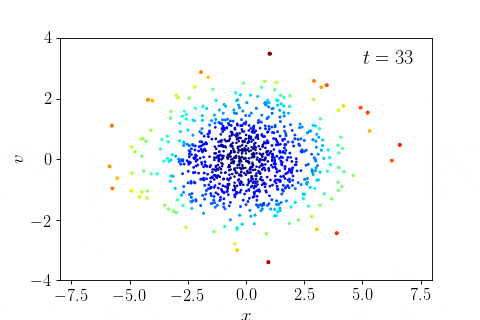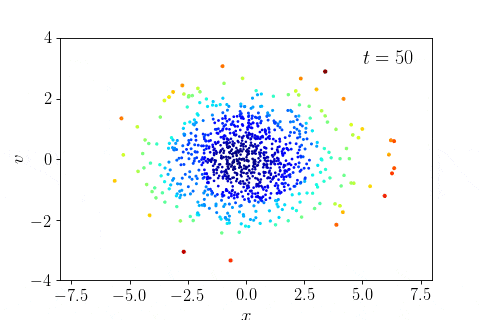
- Phase mixing and violent relaxation in one dimension: example notebook (run locally to see movies, or view on nbviewer)
- A self-gravitating, sech2 disk: example notebook (run locally to see movies, or view on nbviewer)
- The Gaia phase-space spiral: example notebook (run locally to see movies, or view on nbviewer)
- Adiabatic contraction: example notebook (run locally to see movies, or view on nbviewer)
- Adiabatic vs. non-adiabatic energy injection for an exponential disk: example notebook (run locally to see movies, or view on nbviewer)
-
wendyscaling with particle number: example notebook (view on nbviewer)